Iterated forcing

In mathematics, iterated forcing is a method for constructing models of set theory by repeating Cohen's forcing method a transfinite number of times. Iterated forcing was introduced by Solovay and Tennenbaum (1971) in their construction of a model of set theory with no Suslin tree. They also showed that iterated forcing can construct models where Martin's axiom holds and the continuum is any given regular cardinal.

In iterated forcing, one has a transfinite sequence P_α of forcing notions indexed by some ordinals α, which give a family of Boolean-valued models V^P_α. If α+1 is a successor ordinal then P_α+1 is often constructed from P_α using a forcing notion in V^P_α, while if α is a limit ordinal then P_α is often constructed as some sort of limit (such as the direct limit) of the P_β for β<α.

A key consideration is that, typically, it is necessary that 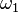$\omega_1$ is not collapsed. This is often accomplished by the use of a preservation theorem such as:

+ Finite support iteration of c.c.c. forcings (see countable chain condition) are c.c.c. and thus preserve 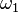$\omega_1$ .

+ Countable support iterations of proper forcings are proper (see Fundamental Theorem of Proper Forcing) and thus preserve 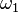$\omega_1$ .

+ Revised countable support iterations of semi-proper forcings are semi-proper and thus preserve 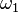$\omega_1$ .

Some non-semi-proper forcings, such as Namba forcing, can be iterated with appropriate cardinal collapses while preserving 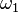$\omega_1$ using methods developed by Saharon Shelah^[1]^[2]^[3]

References

↑ Shelah, S., Proper and Improper Forcing, Springer 1992
↑ Schlindwein, Chaz, Shelah's work on non-semiproper iterations I, Archive for Mathematical Logic (47) 2008 pp. 579 -- 606
↑ Schlindwein, Chaz, Shelah's work on non-semiproper iterations II, Journal of Symbolic Logic (66) 2001, pp. 1865 -- 1883

Jech, Thomas (2003), Set Theory: Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7
Kunen, Kenneth (1980), Set Theory: An Introduction to Independence Proofs, Elsevier, ISBN 978-0-444-86839-8
Shelah, Saharon (1998) [1982], Proper and improper forcing, Perspectives in Mathematical Logic (2 ed.), Berlin: Springer-Verlag, ISBN 3-540-51700-6, MR 1623206
Solovay, R. M.; Tennenbaum, S. (1971). "Iterated Cohen extensions and Souslin's problem". Ann. Of Math. (2) (Annals of Mathematics) 94 (2): 201–245. doi:10.2307/1970860. JSTOR 1970860.

External links

Eisworth, Todd; Moore, Justin Tatch (2009), Milovich, David, ed., ITERATED FORCING AND THE CONTINUUM HYPOTHESIS, Appalachian Set Theory Workshop lecture notes