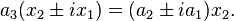Isotropic line

In the geometry of quadratic forms, an isotropic line or null line is a line for which the quadratic form applied to the displacement vector between any pair of its points is zero. An isotropic line occurs only with an isotropic quadratic form, and never with a definite quadratic form.

In the complex projective plane, points are represented by homogeneous coordinates 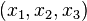(x_1, x_2, x_3) and lines by homogeneous coordinates 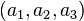(a_1, a_2, a_3). An isotropic line in the complex projective plane satisfies the equation:[1]

a_3(x_2 \pm i x_1) = (a_2 \pm i a_1) x_2 .

In terms of the affine subspace x3 = 1, an isotropic line through the origin is

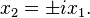x_2 = \pm i x_1 . Attempts to compute the distance between two points on an isotropic line result in zero. In projective geometry, the isotropic lines are the ones passing through the circular points at infinity.

In geology, isotropic lines "separate mutually orthogonal principle trajectories on each side. In a plane-strain field, the strain is zero at isotropic points and lines, and they can be termed neutral points and neutral lines."[2]

See also

References

  1. ↑ C. E. Springer (1964) Geometry and Analysis of Projective Spaces, page 141, W. H. Freeman and Company
  2. ↑ Jean-Pierre Brun (1983) "Isotropic points and lines in strain fields", Journal of Structural Geology 5(3):321–7