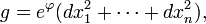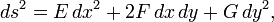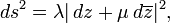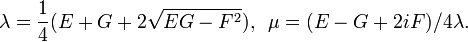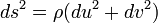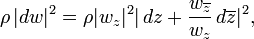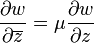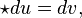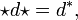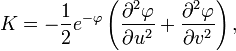Isothermal coordinates

In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifold are local coordinates where the metric is conformal to the Euclidean metric. This means that in isothermal coordinates, the Riemannian metric locally has the form

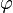g = e^\varphi (dx_1^2 + \cdots + dx_n^2),

where $\varphi$ is a smooth function.

Isothermal coordinates on surfaces were first introduced by Gauss. Korn and Lichtenstein proved that isothermal coordinates exist around any point on a two dimensional Riemannian manifold. On higher-dimensional Riemannian manifolds a necessary and sufficient condition for their local existence is the vanishing of the Weyl tensor and of the Cotton tensor.

Isothermal coordinates on surfaces

Gauss (1822) proved the existence of isothermal coordinates on an arbitrary surface with a real analytic metric, following results of Lagrange (1779) on surfaces of revolution. Results for Hölder continuous metrics were obtained by Korn (1916) and Lichtenstein (1916). Later accounts were given by Morrey (1938), Ahlfors (1955), Bers (1952) and Chern (1955). A particularly simple account using the Hodge star operator is given in DeTurck & Kazdan (1981).

Beltrami equation

The existence of isothermal coordinates can be proved^[1] by applying known existence theorems for the Beltrami equation, which rely on L^p estimates for singular integral operators of Calderon and Zygmund.^[2]^[3] A simpler approach to the Beltrami equation has been given more recently by the late Adrien Douady.^[4]

If the Riemannian metric is given locally as

ds^2 = E \, dx^2 + 2F \, dx \, dy + G \, dy^2,

then in the complex coordinate z = x + iy, it takes the form

ds^2 = \lambda| \, dz +\mu \, d\overline{z}|^2,

where λ and μ are smooth with λ > 0 and |μ| < 1. In fact

\lambda={1\over 4} ( E + G +2\sqrt{EG -F^2}),\,\,\, \mu=(E - G + 2iF)/4\lambda.

In isothermal coordinates (u, v) the metric should take the form

ds^2 = \rho (du^2 + dv^2)

with ρ > 0 smooth. The complex coordinate w = u + i v satisfies

\rho \, |dw|^2 = \rho |w_{z}|^2 | \, dz + {w_{\overline {z}}\over w_z} \, d\overline{z}|^2,

so that the coordinates (u, v) will be isothermal if the Beltrami equation

{\partial w\over \partial \overline{z}} = \mu {\partial w\over \partial z}

has a diffeomorphic solution. Such a solution has been proved to exist in any neighbourhood where ||μ||_∞ < 1.

Hodge star operator

New coordinates u and v are isothermal provided that

\star du =dv,

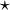where $\star$ is the Hodge star operator defined by the metric.^[5]

Let 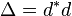$\Delta=d^*d$ be the Laplace–Beltrami operator on functions.

Then by standard elliptic theory, u can be chosen to be harmonic near a given point, i.e. Δ u = 0, with du non-vanishing.

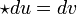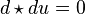By the Poincaré lemma $\star du=dv$ has a local solution v exactly when $d\star d u =0$ .

Since

\star d \star = d^*,

this is equivalent to Δ u = 0, and hence a local solution exists.

Since du is non-zero and the square of the Hodge star operator is −1 on 1-forms, du and dv are necessarily linearly independent, and therefore give local isothermal coordinates.

Gaussian curvature

In the isothermal coordinates (u, v), the Gaussian curvature takes the simpler form

K = -\frac{1}{2} e^{-\varphi} \left(\frac{\partial^2 \varphi}{\partial u^2} + \frac{\partial^2 \varphi}{\partial v^2}\right),

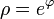where $\rho = e^\varphi$ .

Notes

↑ Imayoshi & Taniguchi 1992, pp. 20–21
↑ Ahlfors 1966, pp. 85–115
↑ Imayoshi & Taniguchi 1992, pp. 92–104
↑ Douady & Buff 2000
↑ DeTurck & Kazdan 1981; Taylor 1996, pp. 377–378

References

Ahlfors, Lars V. (1952), Conformality with respect to Riemannian metrics., Ann. Acad. Sci. Fenn. Ser. A. I. 206, pp. 1–22
Ahlfors, Lars V. (1966), Lectures on quasiconformal mappings, Van Nostrand
Bers, Lipman (1952), Riemann Surfaces, 1951–1952, New York University, pp. 15–35
Chern, Shiing-shen (1955), "An elementary proof of the existence of isothermal parameters on a surface", Proc. Amer. Math. Soc. (American Mathematical Society) 6 (5): 771–782, doi:10.2307/2032933, JSTOR 2032933
DeTurck, Dennis M.; Kazdan, Jerry L. (1981), "Some regularity theorems in Riemannian geometry", Annales Scientifiques de l'École Normale Supérieure. Quatrième Série 14 (3): 249–260, ISSN 0012-9593, MR 644518 .
do Carmo, Manfredo (1976), Differential Geometry of Curves and Surfaces, Prentice Hall, ISBN 0-13-212589-7
Douady, Adrien; Buff, X. (2000), Le théorème d'intégrabilité des structures presque complexes. [Integrability theorem for almost complex structures], London Math. Soc. Lecture Note Ser. 274, Cambridge Univ. Press, pp. 307–324
Gauss, C.F. (1822), On Conformal Representation, translator Smith, Eugene, pp. 463–475
Imayoshi, Y.; Taniguchi, M. (1992), An Introduction to Teichmüller spaces, Springer-Verlag, ISBN 0-387-70088-9
Korn, A. (1916), Zwei Anwendungen der Methode der sukzessiven Annäherungen, Schwarz Abhandlungen, pp. 215–219
Lagrange, J. (1779), Sur la construction des cartes géographiques
Lichtenstein, L. (1916), "Zur Theorie der konformen Abbildung", Bull. Internat. Acad. Sci. Cracovie. Cl. Sci. Math. Nat. Sér. A.: 192–217
Morrey, Charles B. (1938), "On the solutions of quasi-linear elliptic partial differential equations", Trans. Amer. Math. Soc. (American Mathematical Society) 43 (1): 126–166, doi:10.2307/1989904, JSTOR 1989904
Spivak, Michael, A Comprehensive Introduction to Differential Geometry 4 (3 ed.), Publish or Perish, pp. 314–346
Taylor, Michael E. (1996), Partial Differential Equations: Basic Theory, Springer-Verlag, pp. 376–378, ISBN 0-387-94654-3

External links

Hazewinkel, Michiel, ed. (2001), "Isothermal coordinates", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4