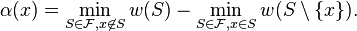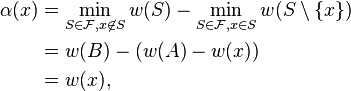Isolation lemma
In theoretical computer science, the term isolation lemma (or isolating lemma) refers to randomized algorithms that reduce the number of solutions to a problem to one, should a solution exist. This is achieved by constructing random constraints such that, with non-negligible probability, exactly one solution satisfies these additional constraints if the solution space is not empty. Isolation lemmas have important applications in computer science, such as the Valiant–Vazirani theorem and Toda's theorem in computational complexity theory.
The first isolation lemma was introduced by Valiant & Vazirani (1986), albeit not under that name. Their isolation lemma chooses a random number of random hyperplanes, and has the property that, with non-negligible probability, the intersection of any fixed non-empty solution space with the chosen hyperplanes contains exactly one element. This suffices to show the Valiant–Vazirani theorem: there exists a randomized polynomial-time reduction from the satisfiability problem for Boolean formulas to the problem of detecting whether a Boolean formula has a unique solution. Mulmuley, Vazirani & Vazirani (1987) introduced an isolation lemma of a slightly different kind: Here every coordinate of the solution space gets assigned a random weight in a certain range of integers, and the property is that, with non-negligible probability, there is exactly one element in the solution space that has minimum weight. This can be used to obtain a randomized parallel algorithm for the maximum matching problem.
Stronger isolation lemmas have been introduced in the literature to fit different needs in various settings. For example, the isolation lemma of Chari, Rohatgi & Srinivasan (1993) has similar guarantees as that of Mulmuley et al., but it uses fewer random bits. In the context of the exponential time hypothesis, Calabro et al. (2008) prove an isolation lemma for k-CNF formulas.
The isolation lemma of Mulmuley, Vazirani, and Vazirani

- Lemma. Let
 and
and  be positive integers, and let
be positive integers, and let 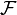 be an arbitrary family of subsets of the universe
be an arbitrary family of subsets of the universe 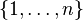 . Suppose each element
. Suppose each element 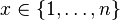 in the universe receives an integer weight
in the universe receives an integer weight 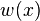 , each of which is chosen independently and uniformly at random from
, each of which is chosen independently and uniformly at random from 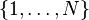 . The weight of a set S in
. The weight of a set S in 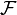 is defined as
is defined as
- Then, with probability at least
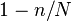 , there is a unique set in
, there is a unique set in 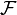 that has the minimum weight among all sets of
that has the minimum weight among all sets of 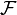 .
.
It is remarkable that the lemma assumes nothing about the nature of the family 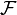 : for instance
: for instance 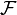 may include all
may include all 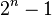 nonempty subsets. Since the weight of each set in
nonempty subsets. Since the weight of each set in 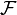 is between
is between 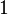 and
and 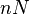 on average there will be
on average there will be 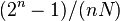 sets of each possible weight.
Still, with high probability, there is a unique set that has minimum weight.
sets of each possible weight.
Still, with high probability, there is a unique set that has minimum weight.
Suppose we have fixed the weights of all elements except an element x. Then x has a threshold weight α, such that if the weight w(x) of x is greater than α, then it is not contained in any minimum-weight subset, and if 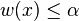 , then it is contained in some sets of minimum weight. Further, observe that if
, then it is contained in some sets of minimum weight. Further, observe that if 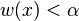 , then every minimum-weight subset must contain x (since, when we decrease w(x) from α, sets that do not contain x do not decrease in weight, while those that contain x do). Thus, ambiguity about whether a minimum-weight subset contains x or not can happen only when its weight is exactly equal to its threshold; in this case we will call x "singular". Now, as the threshold of x was defined only in terms of the weights of the other elements, it is independent of w(x), and therefore, as w(x) is chosen uniformly from {1, …, N},
, then every minimum-weight subset must contain x (since, when we decrease w(x) from α, sets that do not contain x do not decrease in weight, while those that contain x do). Thus, ambiguity about whether a minimum-weight subset contains x or not can happen only when its weight is exactly equal to its threshold; in this case we will call x "singular". Now, as the threshold of x was defined only in terms of the weights of the other elements, it is independent of w(x), and therefore, as w(x) is chosen uniformly from {1, …, N},
and the probability that some x is singular is at most n/N. As there is a unique minimum-weight subset iff no element is singular, the lemma follows.
Remark: The lemma holds with 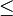 (rather than =) since it is possible that some x has no threshold value (i.e., x will not be in any minimum-weight subset even if w(x) gets the minimum possible value, 1).
(rather than =) since it is possible that some x has no threshold value (i.e., x will not be in any minimum-weight subset even if w(x) gets the minimum possible value, 1).
This is a restatement version of the above proof, due to Joel Spencer (1995).[1]
For any element x in the set, define
Observe that 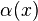 depends only on the weights of elements other than x, and not on w(x) itself. So whatever the value of
depends only on the weights of elements other than x, and not on w(x) itself. So whatever the value of 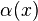 , as w(x) is chosen uniformly from {1, …, N}, the probability that it is equal to
, as w(x) is chosen uniformly from {1, …, N}, the probability that it is equal to 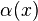 is at most 1/N. Thus the probability that
is at most 1/N. Thus the probability that 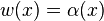 for some x is at most n/N.
for some x is at most n/N.
Now if there are two sets A and B in 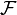 with minimum weight, then, taking any x in A\B, we have
with minimum weight, then, taking any x in A\B, we have
and as we have seen, this event happens with probability at most n/N.
Examples/applications
- The original application was to minimum-weight (or maximum-weight) perfect matchings in a graph. Each edge is assigned a random weight in {1, …, 2m}, and
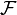 is the set of perfect matchings, so that with probability at least 1/2, there exists a unique perfect matching. When each indeterminate
is the set of perfect matchings, so that with probability at least 1/2, there exists a unique perfect matching. When each indeterminate 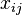 in the Tutte matrix of the graph is replaced with
in the Tutte matrix of the graph is replaced with 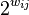 where
where 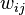 is the random weight of the edge, we can show that the determinant of the matrix is nonzero, and further use this to find the matching.
is the random weight of the edge, we can show that the determinant of the matrix is nonzero, and further use this to find the matching. - More generally, the paper also observed that any search problem of the form "Given a set system
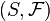 , find a set in
, find a set in 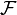 " could be reduced to a decision problem of the form "Is there a set in
" could be reduced to a decision problem of the form "Is there a set in 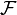 with total weight at most k?". For instance, it showed how to solve the following problem posed by Papadimitriou and Yannakakis, for which (as of the time the paper was written) no deterministic polynomial-time algorithm is known: given a graph and a subset of the edges marked as "red", find a perfect matching with exactly k red edges.
with total weight at most k?". For instance, it showed how to solve the following problem posed by Papadimitriou and Yannakakis, for which (as of the time the paper was written) no deterministic polynomial-time algorithm is known: given a graph and a subset of the edges marked as "red", find a perfect matching with exactly k red edges. - The Valiant–Vazirani theorem, concerning unique solutions to NP-complete problems, has a simpler proof using the isolation lemma. This is proved by giving a randomized reduction from CLIQUE to UNIQUE-CLIQUE.[2]
- Ben-David, Chor & Goldreich (1989) use the proof of Valiant-Vazirani in their search-to-decision reduction for average-case complexity.
- Avi Wigderson used the isolation lemma in 1994 to give a randomized reduction from NL to UL, and thereby prove that NL/poly ⊆ ⊕L/poly.[3] Reinhardt and Allender later used the isolation lemma again to prove that NL/poly = UL/poly.[4]
- The book by Hemaspaandra and Ogihara has a chapter on the isolation technique, including generalizations.[5]
- The isolation lemma has been proposed as the basis of a scheme for digital watermarking.[6]
- There is ongoing work on derandomizing the isolation lemma in specific cases[7] and on using it for identity testing.[8]
Notes
References
- Arvind, V.; Mukhopadhyay, Partha (2008). Derandomizing the Isolation Lemma and Lower Bounds for Circuit Size. Proceedings of the 11th international workshop, APPROX 2008, and 12th international workshop, RANDOM 2008 on Approximation, Randomization and Combinatorial Optimization: Algorithms and Techniques. Boston, MA, USA: Springer-Verlag. pp. 276–289. arXiv:0804.0957. ISBN 978-3-540-85362-6. Retrieved 2010-05-10.
- Arvind, V.; Mukhopadhyay, Partha; Srinivasan, Srikanth (2008). New Results on Noncommutative and Commutative Polynomial Identity Testing. Proceedings of the 2008 IEEE 23rd Annual Conference on Computational Complexity. IEEE Computer Society. pp. 268–279. arXiv:0801.0514. ISBN 978-0-7695-3169-4. Retrieved 2010-05-10.
- Ben-David, S.; Chor, B.; Goldreich, O. (1989). On the theory of average case complexity. Proceedings of the twenty-first annual ACM symposium on Theory of computing - STOC '89. p. 204. doi:10.1145/73007.73027. ISBN 0897913078.
- Calabro, C.; Impagliazzo, R.; Kabanets, V.; Paturi, R. (2008). "The complexity of Unique k-SAT: An Isolation Lemma for k-CNFs". Journal of Computer and System Sciences 74 (3): 386. doi:10.1016/j.jcss.2007.06.015.
- Chari, S.; Rohatgi, P.; Srinivasan, A. (1993). Randomness-optimal unique element isolation, with applications to perfect matching and related problems. Proceedings of the twenty-fifth annual ACM symposium on Theory of computing - STOC '93. p. 458. doi:10.1145/167088.167213. ISBN 0897915917.
- Hemaspaandra, Lane A.; Ogihara, Mitsunori (2002). "Chapter 4. The Isolation Technique". The complexity theory companion. Springer. ISBN 978-3-540-67419-1.
- Majumdar, Rupak; Wong, Jennifer L. (2001). Watermarking of SAT using combinatorial isolation lemmas. Proceedings of the 38th annual Design Automation Conference. Las Vegas, Nevada, United States: ACM. pp. 480–485. doi:10.1145/378239.378566. ISBN 1-58113-297-2. Retrieved 2010-05-10.
- Reinhardt, K.; Allender, E. (2000). "Making Nondeterminism Unambiguous". SIAM Journal on Computing 29 (4): 1118. doi:10.1137/S0097539798339041.
- Mulmuley, Ketan; Vazirani, Umesh; Vazirani, Vijay (1987). "Matching is as easy as matrix inversion". Combinatorica 7 (1): 105–113. doi:10.1007/BF02579206.
- Jukna, Stasys (2001). Extremal combinatorics: with applications in computer science. Springer. pp. 147–150. ISBN 978-3-540-66313-3.
- Valiant, L.; Vazirani, V. (1986). "NP is as easy as detecting unique solutions". Theoretical Computer Science 47: 85–93. doi:10.1016/0304-3975(86)90135-0.
- Wigderson, Avi (1994). NL/poly ⊆ ⊕L/poly. Proceedings of the 9th Structures in Complexity Conference. pp. 59–62.
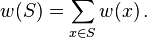
![\Pr[x\text{ is singular}] = \Pr[w(x) = \alpha] \le 1/N](../I/m/92a4b76a7f93f930d85510853d3627cc.png)