Isolated singularity

In complex analysis, a branch of mathematics, an isolated singularity is one that has no other singularities close to it. In other words, a complex number z₀ is an isolated singularity of a function f if there exists an open disk D centered at z₀ such that f is holomorphic on D \ {z₀}, that is, on the set obtained from D by taking z₀ out.

Formally, and within the general scope of functional analysis, an isolated singularity for a function $f$ is any topologically isolated point within an open set where the function is defined.

Every singularity of a meromorphic function is isolated, but isolation of singularities is not alone sufficient to guarantee a function is meromorphic. Many important tools of complex analysis such as Laurent series and the residue theorem require that all relevant singularities of the function be isolated. There are three types of singularities: removable singularities, poles and essential singularities.

Examples

The function $\frac {1} {z}$ has 0 as an isolated singularity.

The cosecant function 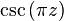$\csc \left(\pi z\right)$ has every integer as an isolated singularity.

Nonisolated singularities

Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. Namely, two kinds of nonisolated singularities exist:

Cluster points, i.e. limit points of isolated singularities: if they are all poles, despite admitting Laurent series expansions on each of them, no such expansion is possible at its limit.

Natural boundaries, i.e. any non-isolated set (e.g. a curve) which functions cannot be analytically continued around (or outside them if they are closed curves in the Riemann sphere).

Examples

The natural boundary of this power series is the unit circle (read examples).

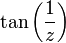The function $\tan\left(\frac{1}{z}\right)$ is meromorphic in 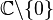$\mathbb{C}\backslash\{0\}$ , with simple poles in 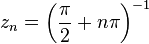$z_n=\left(\frac{\pi}{2}+n\pi\right)^{-1}$ , for every 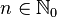$n\in\mathbb{N}_0$ . Since 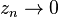$z_n\rightarrow 0$ , every punctured disk centred in 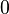$0$ has an infinite number of singularities within, so no Laurent espansion is available for 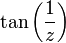$\tan\left(\frac{1}{z}\right)$ around 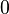$0$ , which is in fact a cluster point of its.

The function 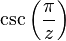$\csc \left(\frac {\pi} {z}\right)$ has a singularity at 0 which is not isolated, since there are additional singularities at the reciprocal of every integer which are located arbitrarily close to 0 (though the singularities at these reciprocals are themselves isolated).

The function here defined as the Maclaurin series 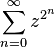$\sum_{n=0}^{\infty}z^{2^n}$ converges inside the open unit disk centred at 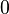$0$ and has the unit circle as its natural boundary.

Isolated singularity

Examples

Nonisolated singularities

Examples

See also

External links