Irrational winding of a torus

In topology, a branch of mathematics, an irrational winding of a torus is a continuous injection of a line into a torus that is used to set up several counterexamples.[1] A related notion is the Kronecker foliation of a torus, a foliation formed by the set of all translates of a given irrational winding.

Definition

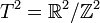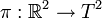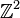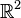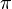One way of constructing a torus is as the quotient space T^2 = \mathbb{R}^2 / \mathbb{Z}^2 of a two-dimensional real vector space by the additive subgroup of integer vectors, with the corresponding projection \pi: \mathbb{R}^2 \to T^2. Each point in the torus has as its preimage one of the translates of the square lattice \mathbb{Z}^2 in \mathbb{R}^2, and \pi factors through a map that takes any point in the plane to a point in the unit square 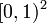[0, 1)^2 given by the fractional parts of the original point's Cartesian coordinates. Now consider a line in 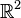\mathbb{R}^2 given by the equation y = kx. If the slope k of the line is rational, then it can be represented by a fraction and a corresponding lattice point of 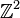\mathbb{Z}^2. It can be shown that then the projection of this line is a simple closed curve on a torus. If, however, k is irrational, then it will not cross any lattice points except 0, which means that its projection on the torus will not be a closed curve, and the restriction of 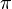\pi on this line is injective. Moreover, it can be shown that the image of this restricted projection as a subspace, called the irrational winding of a torus, is dense in the torus.

Applications

Irrational windings of a torus may be used to set up counter-examples related to monomorphisms. An irrational winding is an immersed submanifold but not a regular submanifold of the torus, which shows that the image of a manifold under a continuous injection to another manifold is not necessarily a (regular) submanifold.[2] Irrational windings are also examples of the fact that the induced submanifold topology does not have to coincide with the subspace topology of the submanifold [2] a[›]

Secondly, the torus can be considered as a Lie group 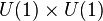U(1) \times U(1), and the line can be considered as 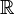\mathbb{R}. Then it is easy to show that the image of the continuous and analytic group homomorphism 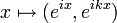x \mapsto (e^{ix}, e^{ikx}) is not a Lie subgroup[2][3] (because it's not closed in the torus – see the closed subgroup theorem) while, of course, it is still a group. It may also be used to show that if a subgroup H of the Lie group G is not closed, the quotient G/H does not need to be a submanifold[4] and might even fail to be a Hausdorff space.

See also

Notes

^ a: As a topological subspace of the torus, the irrational winding is not a manifold at all, because it is not locally homeomorphic to 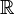\mathbb{R}

References

  1. ↑ D. P. Zhelobenko. Compact Lie groups and their representations.
  2. ↑ 2.0 2.1 2.2 Loring W. Tu (2010). An Introduction to Manifolds. Springer. p. 168. ISBN 978-1-4419-7399-3.
  3. ↑ Čap, Andreas; Slovák, Jan (2009), Parabolic Geometries: Background and general theory, AMS, p. 24, ISBN 978-0-8218-2681-2
  4. ↑ Sharpe, R.W. (1997), Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer-Verlag, New York, p. 146, ISBN 0-387-94732-9