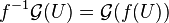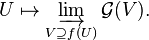Inverse image functor
In mathematics, the inverse image functor is a covariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.
| Image functors for sheaves |
|---|
| direct image f∗ |
| inverse image f∗ |
| direct image with compact support f! |
| exceptional inverse image Rf! |
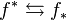 |
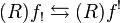 |
Definition
Suppose given a sheaf 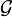 on
on  and that we want to transport
and that we want to transport 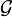 to
to  using a continuous map
using a continuous map 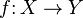 .
.
We will call the result the inverse image or pullback sheaf 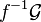 . If we try to imitate the direct image by setting
. If we try to imitate the direct image by setting
for each open set  of
of  , we immediately run into a problem:
, we immediately run into a problem: 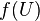 is not necessarily open. The best we could do is to approximate it by open sets, and even then we will get a presheaf and not a sheaf. Consequently, we define
is not necessarily open. The best we could do is to approximate it by open sets, and even then we will get a presheaf and not a sheaf. Consequently, we define 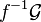 to be the sheaf associated to the presheaf:
to be the sheaf associated to the presheaf:
(Here  is an open subset of
is an open subset of  and the colimit runs over all open subsets
and the colimit runs over all open subsets  of
of  containing
containing 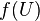 .)
.)
For example, if  is just the inclusion of a point
is just the inclusion of a point  of
of  , then
, then 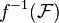 is just the stalk of
is just the stalk of  at this point.
at this point.
The restriction maps, as well as the functoriality of the inverse image follows from the universal property of direct limits.
When dealing with morphisms 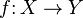 of locally ringed spaces, for example schemes in algebraic geometry, one often works with sheaves of
of locally ringed spaces, for example schemes in algebraic geometry, one often works with sheaves of 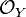 -modules, where
-modules, where 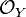 is the structure sheaf of
is the structure sheaf of  . Then the functor
. Then the functor 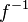 is inappropriate, because in general it does not even give sheaves of
is inappropriate, because in general it does not even give sheaves of 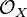 -modules. In order to remedy this, one defines in this situation for a sheaf of
-modules. In order to remedy this, one defines in this situation for a sheaf of 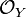 -modules
-modules 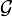 its inverse image by
its inverse image by
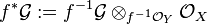 .
.
Properties
- While
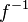 is more complicated to define than
is more complicated to define than 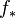 , the stalks are easier to compute: given a point
, the stalks are easier to compute: given a point 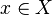 , one has
, one has 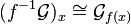 .
. -
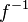 is an exact functor, as can be seen by the above calculation of the stalks.
is an exact functor, as can be seen by the above calculation of the stalks. -
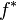 is (in general) only right exact. If
is (in general) only right exact. If 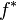 is exact, f is called flat.
is exact, f is called flat. -
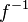 is the left adjoint of the direct image functor
is the left adjoint of the direct image functor 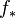 . This implies that there are natural unit and counit morphisms
. This implies that there are natural unit and counit morphisms 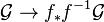 and
and 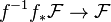 . These morphisms yield a natural adjunction correspondence:
. These morphisms yield a natural adjunction correspondence:
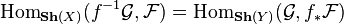 .
.
However, these morphisms are almost never isomorphisms.
For example, if 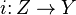 denotes the inclusion of a closed subset, the stalks of
denotes the inclusion of a closed subset, the stalks of 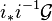 at a point
at a point 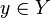 is canonically isomorphic to
is canonically isomorphic to 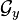 if
if  is in
is in  and
and  otherwise. A similar adjunction holds for the case of sheaves of modules, replacing
otherwise. A similar adjunction holds for the case of sheaves of modules, replacing 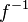 by
by 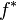 .
.