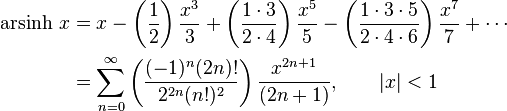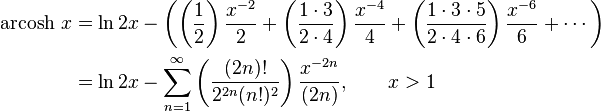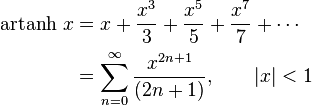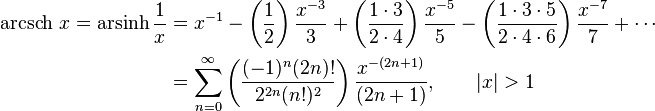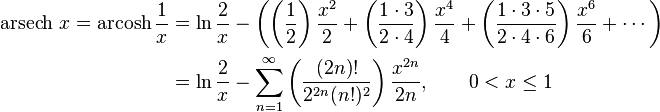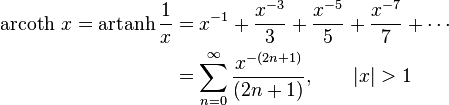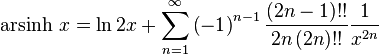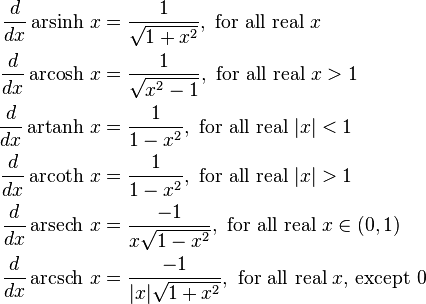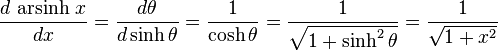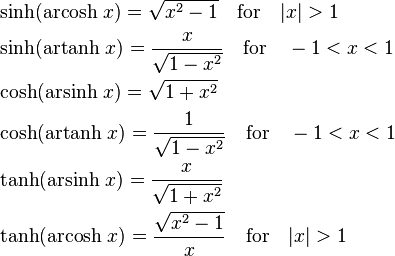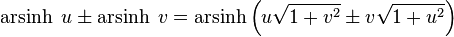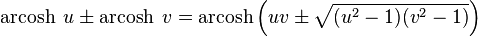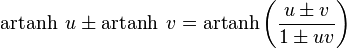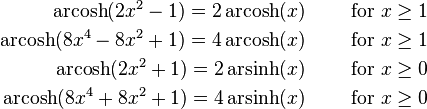Inverse hyperbolic function

The inverse hyperbolic functions.

In mathematics, the inverse hyperbolic functions provide a hyperbolic angle corresponding to a given value of a hyperbolic function. The size of the hyperbolic angle is equal to the area of the corresponding hyperbolic sector of the hyperbola xy = 1, or twice the area of the corresponding sector of the unit hyperbola x2 − y2 = 1, just as a circular angle is twice the area of the circular sector of the unit circle. Some authors have called inverse hyperbolic functions "area functions" to realize the hyperbolic angles.

The preferred abbreviations are arsinh, arcosh, etc.; however, arcsinh, arccosh, etc., are also commonly seen by analogy with the nomenclature for inverse trigonometric functions. The latter are misnomers, since the prefix arc is the abbreviation for arcus, while the prefix ar stands for area.[1][2] [3] Other authors prefer to use the notation argsinh, argcosh, argtanh, and so on, where the prefix arg is the abbreviation of the Latin argumentum.[4] In computer science this is often shortened to asinh. The notation sinh−1(x), cosh−1(x), etc., is also used,[5] despite the fact that care must be taken to avoid misinterpretations of the superscript −1 as a power as opposed to a shorthand for inverse (e.g., cosh−1(x) versus cosh(x)−1).

Logarithmic representation

The operators are defined in the complex plane by:

\begin{align} \operatorname{arsinh}\, z &= \ln(z + \sqrt{z^2 + 1} \,) \\[2.5ex] \operatorname{arcosh}\, z &= \ln(z + \sqrt{z+1} \sqrt{z-1} \,) \\[1.5ex] \operatorname{artanh}\, z &= \tfrac12\ln\left({1+z}\right) - \tfrac12\ln\left({1-z}\right) \\ \operatorname{arcoth}\, z &= \tfrac12\ln\left({1+\frac{1}{z} }\right) - \tfrac12\ln\left({1-\frac{1}{z}}\right) \\ \operatorname{arcsch}\, z &= \ln\left( \frac{1}{z} + \sqrt{ \frac{1}{z^2} +1 } \,\right) \\ \operatorname{arsech}\, z &= \ln\left( \frac{1}{z} + \sqrt{ \frac{1}{z} + 1 } \, \sqrt{ \frac{1}{z} -1 } \,\right) \end{align}

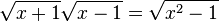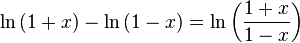The above square roots are principal square roots, and the logarithm function is the complex logarithm. For real arguments, i.e., z = x, which return real values, certain simplifications can be made e.g. \sqrt{x+1}\sqrt{x-1}=\sqrt{x^2-1} and \ln\left({1+x}\right) - \ln\left({1-x}\right) = \ln\left(\frac{1+x}{1-x}\right), which are not generally true for complex arguments.

Square representing central portion of the complex z-plane painted in psychedelic colours
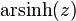
\operatorname{arsinh}(z)
Square representing central portion of the complex z-plane painted in psychedelic colours
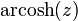
\operatorname{arcosh}(z)
Square representing central portion of the complex z-plane painted in psychedelic colours
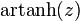
\operatorname{artanh}(z)
Square representing central portion of the complex z-plane painted in psychedelic colours
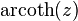
\operatorname{arcoth}(z)
Square representing central portion of the complex z-plane painted in psychedelic colours
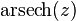
\operatorname{arsech}(z)
Square representing central portion of the complex z-plane painted in psychedelic colours
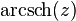
\operatorname{arcsch}(z)
Inverse hyperbolic functions in the complex z-plane: the colour at each point in the plane represents the complex value of the respective function at that point

Series expansions

Expansion series can be obtained for the above functions:

\begin{align}\operatorname{arsinh}\, x & = x - \left( \frac {1} {2} \right) \frac {x^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^5} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^7} {7} +\cdots \\ & = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n+1}} {(2n+1)} , \qquad \left| x \right| < 1 \end{align}
\begin{align}\operatorname{arcosh}\, x & = \ln 2x - \left( \left( \frac {1} {2} \right) \frac {x^{-2}} {2} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-4}} {4} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-6}} {6} +\cdots \right) \\ & = \ln 2x - \sum_{n=1}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-2n}} {(2n)} , \qquad x > 1 \end{align}
\begin{align}\operatorname{artanh}\, x & = x + \frac {x^3} {3} + \frac {x^5} {5} + \frac {x^7} {7} +\cdots \\ & = \sum_{n=0}^\infty \frac {x^{2n+1}} {(2n+1)} , \qquad \left| x \right| < 1 \end{align}
\begin{align}\operatorname{arcsch}\, x = \operatorname{arsinh} \frac1x & = x^{-1} - \left( \frac {1} {2} \right) \frac {x^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-5}} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-7}} {7} +\cdots \\ & = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-(2n+1)}} {(2n+1)} , \qquad \left| x \right| > 1 \end{align}
\begin{align}\operatorname{arsech}\, x = \operatorname{arcosh} \frac1x & = \ln \frac{2}{x} - \left( \left( \frac {1} {2} \right) \frac {x^{2}} {2} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{4}} {4} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{6}} {6} +\cdots \right) \\ & = \ln \frac{2}{x} - \sum_{n=1}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n}} {2n} , \qquad 0 < x \le 1 \end{align}
\begin{align}\operatorname{arcoth}\, x = \operatorname{artanh} \frac1x & = x^{-1} + \frac {x^{-3}} {3} + \frac {x^{-5}} {5} + \frac {x^{-7}} {7} +\cdots \\ & = \sum_{n=0}^\infty \frac {x^{-(2n+1)}} {(2n+1)} , \qquad \left| x \right| > 1 \end{align}

Asymptotic expansion for the arsinh x is given by

\operatorname{arsinh}\, x = \ln 2x + \sum\limits_{n = 1}^\infty {\left( { - 1} \right)^{n - 1} \frac{{\left( {2n - 1} \right)!!}}{{2n\left( {2n} \right)!!}}} \frac{1}{{x^{2n} }}

Derivatives

\begin{align} \frac{d}{dx} \operatorname{arsinh}\, x & {}= \frac{1}{\sqrt{1+x^2}}, \text{ for all real } x\\ \frac{d}{dx} \operatorname{arcosh}\, x & {}= \frac{1}{\sqrt{x^2-1}}, \text{ for all real } x>1\\ \frac{d}{dx} \operatorname{artanh}\, x & {}= \frac{1}{1-x^2}, \text{ for all real } |x|<1\\ \frac{d}{dx} \operatorname{arcoth}\, x & {}= \frac{1}{1-x^2}, \text{ for all real } |x|>1\\ \frac{d}{dx} \operatorname{arsech}\, x & {}= \frac{-1}{x\sqrt{1-x^2}}, \text{ for all real } x \in (0,1)\\ \frac{d}{dx} \operatorname{arcsch}\, x & {}= \frac{-1}{|x|\sqrt{1+x^2}}, \text{ for all real } x\text{, except } 0\\ \end{align}

For an example differentiation: let θ = arsinh x, so:

\frac{d\,\operatorname{arsinh}\, x}{dx} = \frac{d \theta}{d \sinh \theta} = \frac{1} {\cosh \theta} = \frac{1} {\sqrt{1+\sinh^2 \theta}} = \frac{1}{\sqrt{1+x^2}}

Composition of hyperbolic and inverse hyperbolic functions

\begin{align} &\sinh(\operatorname{arcosh}\,x) = \sqrt{x^{2} - 1} \quad \text{for} \quad |x| > 1 \\ &\sinh(\operatorname{artanh}\,x) = \frac{x}{\sqrt{1-x^{2}}} \quad \text{for} \quad -1 < x < 1 \\ &\cosh(\operatorname{arsinh}\,x) = \sqrt{1+x^{2}} \\ &\cosh(\operatorname{artanh}\,x) = \frac{1}{\sqrt{1-x^{2}}} \quad \text{for} \quad -1 < x < 1 \\ &\tanh(\operatorname{arsinh}\,x) = \frac{x}{\sqrt{1+x^{2}}} \\ &\tanh(\operatorname{arcosh}\,x) = \frac{\sqrt{x^{2} - 1}}{x} \quad \text{for} \quad |x| > 1 \end{align}

Addition formulae

\operatorname{arsinh} \;u \pm \operatorname{arsinh} \;v = \operatorname{arsinh} \left(u \sqrt{1 + v^2} \pm v \sqrt{1 + u^2}\right)
\operatorname{arcosh} \;u \pm \operatorname{arcosh} \;v = \operatorname{arcosh} \left(u v \pm \sqrt{(u^2 - 1) (v^2 - 1)}\right)
\operatorname{artanh} \;u \pm \operatorname{artanh} \;v = \operatorname{artanh} \left( \frac{u \pm v}{1 \pm uv} \right)
\begin{align}\operatorname{arsinh} \;u + \operatorname{arcosh} \;v & = \operatorname{arsinh} \left(u v + \sqrt{(1 + u^2) (v^2 - 1)}\right) \\ & = \operatorname{arcosh} \left(v \sqrt{1 + u^2} + u \sqrt{v^2 - 1}\right) \end{align}

Other identities

\begin{align} \operatorname{arcosh}(2x^2-1)=2\operatorname{arcosh}(x) \quad\quad \hbox{ for }x\geq 1 \\ \operatorname{arcosh}(8x^4-8x^2+1)=4\operatorname{arcosh}(x) \quad\quad \hbox{ for }x\geq 1 \\ \operatorname{arcosh}(2x^2+1)=2\operatorname{arsinh}(x) \quad\quad \hbox{ for }x\geq 0 \\ \operatorname{arcosh}(8x^4+8x^2+1)=4\operatorname{arsinh}(x) \quad\quad \hbox{ for }x\geq 0 \end{align}

See also

References

  1. ↑ As stated by Jan Gullberg, Mathematics: From the Birth of Numbers (New York: W. W. Norton & Company, 1997), ISBN 0-393-04002-X, p. 539:
    Another form of notation, arcsinh x, arccosh x, etc., is a practice to be condemned as these functions have nothing whatever to do with arc, but with area, as is demonstrated by their full Latin names,

    arsinh     area sinus hyperbolicus
    arcosh     area cosinus hyperbolicus, etc.

  2. ↑ As stated by Eberhard Zeidler, Wolfgang Hackbusch and Hans Rudolf Schwarz, translated by Bruce Hunt, Oxford Users' Guide to Mathematics (Oxford: Oxford University Press, 2004), ISBN 0-19-850763-1, Section 0.2.13: "The inverse hyperbolic functions", p. 68: "The Latin names for the inverse hyperbolic functions are area sinus hyperbolicus, area cosinus hyperbolicus, area tangens hyperbolicus and area cotangens hyperbolicus (of x). ..." This aforesaid reference uses the notations arsinh, arcosh, artanh, and arcoth for the respective inverse hyperbolic functions.
  3. ↑ As stated by Ilja N. Bronshtein, Konstantin A. Semendyayev, Gerhard Musiol and Heiner Muehlig, Handbook of Mathematics (Berlin: Springer-Verlag, 5th ed., 2007), ISBN 3-540-72121-5, doi:10.1007/978-3-540-72122-2, Section 2.10: "Area Functions", p. 91:
    The area functions are the inverse functions of the hyperbolic functions, i.e., the inverse hyperbolic functions. The functions sinh x, tanh x, and coth x are strictly monotone, so they have unique inverses without any restriction; the function cosh x has two monotonic intervals so we can consider two inverse functions. The name area refers to the fact that the geometric definition of the functions is the area of certain hyperbolic sectors ...
  4. ↑ Bacon, Harold Maile (1942). Differential and Integral Calculus. McGraw-Hill. p. 203.
  5. ↑ Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (1992). "Section 5.6. Quadratic and Cubic Equations". Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd ed.). New York: Cambridge University Press. ISBN 0-521-43064-X.

External links