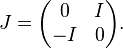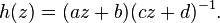Invariant convex cone

In mathematics, an invariant convex cone is a closed convex cone in a Lie algebra of a connected Lie group that is invariant under inner automorphisms. The study of such cones was initiated by Ernest Vinberg and Bertram Kostant.

For a simple Lie algebra, the existence of an invariant convex cone forces the Lie algebra to have a Hermitian structure, i.e. the maximal compact subgroup has center isomorphic to the circle group. The invariant convex cone generated by a generator of the Lie algebra of the center is closed and is the minimal invariant convex cone (up to a sign). The dual cone with respect to the Killing form is the maximal invariant convex cone. Any intermediate cone is uniquely determined by its intersection with the Lie algebra of a maximal torus in a maximal compact subgroup. The intersection is invariant under the Weyl group of the maximal torus and the orbit of every point in the interior of the cone intersects the interior of the Weyl group invariant cone.

For the real symplectic group, the maximal and minimal cone coincide, so there is only one invariant convex cone. When one is properly contained in the other, there is a continuum of intermediate invariant convex cones.

Invariant convex cones arise in the analysis of holomorphic semigroups in the complexification of the Lie group, first studied by Grigori Olshanskii. They are naturally associated with Hermitian symmetric spaces and their associated holomorphic discrete series. The semigroup is made up of those elements in the complexification which, when acting on the Hermitian symmetric space of compact type, leave invariant the bounded domain corresponding to the noncompact dual. The semigroup acts by contraction operators on the holomorphic discrete series; its interior acts by Hilbert–Schmidt operators. The unitary part of their polar decomposition is the operator corresponding to an element in the original real Lie group, while the positive part is the exponential of an imaginary multiple of the infinitesimal operator corresponding to an element in the maximal cone. A similar decomposition already occurs in the semigroup.

The oscillator semigroup of Roger Howe concerns the special case of this theory for the real symplectic group. Historically this has been one of the most important applications and has been generalized to infinite dimensions. This article treats in detail the example of the invariant convex cone for the symplectic group and its use in the study of the symplectic Olshanskii semigroup.

Invariant convex cone in symplectic Lie algebra

The Lie algebra of the symplectic group on R²ⁿ has a unique invariant convex cone. It is self-dual.^[1] The cone and its properties can be derived directly using the description of the symplectic Lie algebra provided by the Weyl calculus in quantum mechanics.^[2] Let the variables in R²ⁿ be x₁, ..., x_n, y₁, ..., y_n. Taking the standard inner product on R²ⁿ, the symplectic form corresponds to the matrix

\displaystyle{J=\begin{pmatrix} 0 & I \\ -I & 0\end{pmatrix}.}

The real polynomials on R²ⁿ form an infinite-dimensional Lie algebra under the Poisson bracket

\displaystyle{\{f,g\}=\sum_i {\partial f\over \partial x_i}{\partial g\over \partial y_i} - {\partial f\over \partial y_i}{\partial g\over \partial x_i}.}

The polynomials of degree ≤ 2 form a finite-dimensional Lie algebra with center the constant polynomials. The homogeneous polynomials of degree 2 form a Lie subalgebra isomorphic to the symplectic Lie algebra. The symplectic group acts naturally on this subalgebra by reparametrization and this yields the adjoint representation. Homogeneous polynomials of degree 2 on the other hand are just symmetric bilinear forms on R_2n. They therefore correspond to symmetric 2n × 2n matrices. The Killing form on the Lie algebra is proportional to the trace form Tr AB. The positive definite symmetric bilinear forms give an open invariant convex cone with closure the set P of positive semi-definite symmetric bilinear forms. Because the Killing form is the trace form, the cone P is self-dual.

Any positive symmetric bilinear form defines a new inner product on R²ⁿ. The symplectic from defines an invertible skew-adjoint operator T with respect to this inner product with –T² a positive operator. An orthonormal basis can be chose so that T has 2 × 2 skew-symmetric matrices down the diagonal. Scaling the orthonormal basis, it follows that there is a symplectic basis for R²ⁿ diagonalizing the original positive symmetric bilinear form. Thus every positive symmetric bilinear form lies in the orbit of a diagonal form under the symplectic group.

If C is any other invariant convex cone then it is invariant under the closed subgroup U of the symplectic group consisting of orthogonal transformations commuting with J. Identifying R²ⁿ with the complex inner product space Cⁿ using the complex structure J, U can be identified with U(n). Taking any non-zero point in C. the average over U with respect to Haar measure lies in C and is non-zero. The corresponding quadratic form is a multiple of the standard inner product. Replacing C by –C this multiple can be taken to be positive. There is a copy of SL(2,R) in the symplectic group acting only on the variables x_i and y_i. These operators can be used to transform $(x i) 2 + (y i) 2$ into $t (x i) 2 + (2 - t)(y i) 2$ with 0 < t < 2. It follows that C contains the point $(x 1) 2 + (y 2) 2 + ... + (y n) 2$ . Applying diagonal scaling operators in the second and subsequent copies of SL(2,R), the cone C must contain the quadratic form $(x 1) 2$ . By invariance C must also contain the quadratic forms $(x i) 2$ and $(y i) 2$ . By convexity it contains all diagonal positive symmetric bilinear forms. Since any positive symmetric bilinear form is in the orbit of a diagonal form, C contains the cone of non-negative symmetric bilinear forms. By duality the dual cone C* is contained in P. If C is a proper cone, the previous argument shows that C* = P and hence that C = P.

This argument shows that every positive definite symmetric form is in the orbit of a form with corresponding quadratic form

\displaystyle{Q(x,y)=\sum a_i (x_i^2+y_i^2),}

with a_i > 0. This corresponds to a cone in the Lie algebra of the (diagonal) maximal torus of U.

Since every element of P is diagonalizable, the stabilizer of a positive element in the symplectic group is contained in a conjugate of U. On the other hand if K is another compact subgroup of the symplectic group, averaging over Haar measure shows that it leaves invariant a positive element of P. Thus K is contained in a conjugate of U. It follows that U is a maximal compact subgroup of the symplectic group and that any other such subgroup must be a conjugate of U.

Decomposition in symplectic Olshanski semigroup

The complex symplectic group acts by Möbius transformations on X, the complex symmetric matrices with operator norm less than or equal to one. Representing an element as a 2 × 2 block matrix $h = \begin{pmatrix} a & b \\ c & d\end{pmatrix}$ , the action is given by

\displaystyle{h(z)=(az+b)(cz+d)^{-1}.}

There is a period 2 automorphism σ of the complex symplectic group with fixed point subgroup the real symplectic group. Then x⁺ = σ(x)^{-1} is an antiautomorphism of H which induces the inverse on the real symplectic group G. If g is in the open Olshanski semigroup H, let h = g⁺g. By Brouwer's fixed point theorem applied to the compact convex set X, g has a fixed point in X. Since g carries X into its interior, the fixed point is an interior point. Since G acts transitively on the interior of X, post-multiplying by an element of G if necessary, it can be assumed that h fixes 0. Since h⁺ = h, it follows that b = c = 0. Conjugating by an element in K ⊂ SU(1,1), a and d can be diagonalized. It has positive eigenvalues, so there is a unique positive diagonal operator h₁ with square h. By uniqueness (h₁)⁺ = h₁. Since h₁ is diagonal, the theory for SU(1,1) and SL(2,C) acting on the unit disk in C shows that h₁ lies in exp C. On the other hand k = g (h₁)⁻¹ satisfies k⁺k = 1 so that σ(k) = k. Thus k lies in G and therefore, using the invariance of C, H admits the decomposition

\displaystyle{H=G\cdot \exp(C) =\exp(C)\cdot G.}

In fact there is a similar decomposition for the closed Olshanski symplectic semigroup:

\displaystyle{\overline{H}=G\cdot \exp(\overline{C}) =\exp(\overline{C})\cdot G.}

Moreover the map (g,x) ↦ g exp x is a homeomorphism.^[3]

In fact if X is in C, it is diagonalizable with real eigenvalues. So that exp X has strictly positive eigenvalues. By continuity if X is in the closure of C, it has real eigenvalues and exp X has strictly positive eigenvalues. Any invertible operator that is a limit of such exp X will also have strictly positive eigenvalues. By the holomorphic functional calculus the exponential map on the space of operators with real spectrum defines a homeomorphism onto the space of operators with strictly positive spectrum, with an analytic inverse given by the logarithm. It follows that $\exp \overline{C}$ is closed in the complex symplectic group.

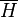If g_n exp X_n tends to h, then exp 2X_n tends to h⁺h. Since $\exp \overline{C}$ is closed, h⁺h = exp 2X for some X and hence h exp –X lies in G. So the closure of $G \exp \overline{C}$ is closed and coincides with $\overline{H}$ . Similarly if g_n exp X_n tends to g exp X, then exp 2 X_n tends to exp 2X. Hence X_n tends to X. But then exp X_n tends to exp X, so that g_n tends to g.

The use of the Brouwer fixed-point theorem can be avoided by applying more direct fixed-point theorems for holomorphic mappings, such as the Earle–Hamilton fixed point theorem and its variants.^[4] In fact a Möbius transformation f taking {z: ||z|| < 1, z^t = z} into a compact subset has a unique fixed point z₀ with fⁿ(z) → z₀ for any z.

Uniqueness follows because, if f has a fixed point, after conjugating by an element of the real symplectic group, it can be assumed to be 0. Then f has the form f(z) = az(1 + cz)⁻¹a^t, where c^t = c, with iterates f^m(z) = a^mz(1 + c_mz)⁻¹(a^m)^t with c_m = c + a^tca + ⋅⋅⋅ + (a^{m − 1})^tca^{m − 1}. Here a and c_m all have operator norm less than one. Thus for ||z|| ≤ r < 1, f^m(z) tends to 0 uniformly, so that in particular 0 is the unique fixed point and it is obtained by applying iterates of f.

Existence of a fixed point for f follows by noting that is an increasing sequence n_k such that f^n_k and f^{n_{2k + 1} − n_2k} are both uniformly convergent on compacta, to h and g respectively. This follows because real symplectic transformations g_n can be chosen so that h_n = g_n ∘ fⁿ fixes 0, with a subsequence of g_n's convergent precisely when the corresponding subsequence of fⁿ(0) is convergent. Since the transformations h_n can be written as h_n(z) = a_nz(1 + b_nz)⁻¹ (a_n)^t, convergent subsequences can be chosen. By construction g ∘ h = h. So points in the image of h are fixed by g. Now g and h are either constant or have the form az(1 + cz)⁻¹a^t followed by a real symplectic transformation. Since the image of h is connected and a non-constant map has just one fixed point, the image of h is a single point z₀, fixed by g. Since g commutes with f, f(z₀) is also fixed by g and hence f(z₀)= z₀, so that z₀ is a fixed point of f.^[5]

Maximality of symplectic Olshanski semigroup

The symplectic group acts transitively by Möbius transformations on the complex symmetric matrices with operator norm less than one. The open Olshanski semigroup consists of Möbius transformations in the complex symplectic group which take the space complex symmetric matrices of norm ≤ 1 into complex symmetric matrices of norm < 1. Its closure is a maximal proper semigroup in the complex symplectic group.

In two dimensions this follows from a general argument of Lawson (1998) which also applies in one dimension. Let G = SL(2,R) act by Möbius transformations on the extended real line and let H be the open semigroup consisting of transformations carrying [–1,1] into (–1,1). Its closure 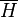$\overline{H}$ is the closed semigroup of transformations carrying [–1,1] into itself. Maximality of 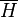$\overline{H}$ is proved by first showing that any strictly larger semigroup S contains an element g sending |t| < 1 onto |t| > 1. In fact if x is in S but not in 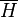$\overline{H}$ , then there is an interval I₁ in I = (–1,1) such that x I₁ lies in [–1,1]^c. Then for some h in H, I₁ = hI. Similarly yxI₁ = [–1,1]^c for some y in H. So g = yxh lies in S and sends I onto [–1,1]^c. It follows that g² fixes I, so that g⁻¹ lies in S. If z lies in H then z g I contains g I. Hence g⁻¹z⁻¹ g lies in 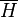$\overline{H}$ . So z⁻¹ lies in S and therefore S contains an open neighbourhood of 1. Hence S = SL(2,R).^[6]

Maximality can be deduced for the Olshanski symplectic semigroup in SL(2,C) from the maximality of this semigroup in SL(2,R). It suffices to show that the closed semigroup contains SL(2,R), because the scaling transformations lie in the interior of the Olshanski symplectic semigroup. So if their inverses lie in the symplectic semigroup, it contains a neighbourhood of the identity and hence the whole of SL(2,C). If S is a semigroup properly containing the symplectic semigroup, it contains an element carrying the closed unit disk outside itself. Pre- and post-composing with elements of SU(1,1), it can be assumed that the element g of S carries 0 into r > 1. Precomposing with a scaling transformation, it can be assumed that g carries the closed unit disk onto a small neighbourhood of r. Pre-composing with an element of SU(1,1), the inverse image of the real axis can be taken to be the diameter joining –1 and 1. But in that case, g must lie in SL(2,R). From the maximality result for semigroups in SL(2,R), S must contain SL(2,R) and hence must be the whole of SL(2,C).^[7]

Autonne–Takagi factorization states that for any complex symmetric matrix M, there is a unitary matrix U such that UMU^t is diagonal.^[8] IfS is a semigroup properly containing the closure of the Olshanki semigroup, then it contains an element g such that z = g(0) with 1< ||z|| < ∞.

Indeed there is an embedding due to Harish-Chandra of the space of complex symmetric n by n matrices as a dense open subset of the compact Grassmannian of Langrangian subspaces of C²ⁿ. Morevoer this embedding is equivariant for the action of the real symplectic group.^[9] In fact, with the standard complex inner product on C²ⁿ, the Grassmannian of n-dimensional subspaces has a continuous transitive action of SL(2n,C) and its maximal compact subpgroup SU(2n). It can be identified with the space of orthogonal rank n projections, a compact subspace of M_2n(C). Taking coordinates (z₁,...,z_n,w₁,...,w_n) on C²ⁿ, the symplectic form is given by

\displaystyle{B((z,w),(z^\prime,w^\prime))=\sum z_iw_i^\prime - w_iz_i^\prime.}

An n-dimensional subspace U is called Lagrangian if B vanishes on U. The Lagrangian subpaces form a closed subset of the Grassmannian on which the complex symplectic group and the unitary symplectic group act transitively. This is the Lagrangian Grassmannian. The subspace U₀ formed of vectors with z_i = 0 is Lagrangian. The set of Langrangian subspaces U for which the restriction of the orthogonal projection onto U₀ is an isomorphism forms an open dense subset Ω of the Lagrangian Grassmannian. Any such subspace has a canonical basis whose column vectors form a 2n by n matrix $\begin{pmatrix} Z\\ I\end{pmatrix}$ where Z is a complex symmetric n by n matrix and I is the n by n identity matrix. 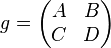Under this correspondence elements of the complex symplectic group, viewed as block matrices $g = \begin{pmatrix} A & B \\ C & D\end{pmatrix}$ act as Möbius transformations, g(Z) = (AZ + B)(CZ + D)⁻¹. The unit ball for the operator norm and its closure are left invariant under the corresponding real form of the symplectic group.

If an element g of the complex symplectic group does not lie in the closure of Olshanski semigroup, it must carry some point W of the open unit ball into the complement of its closure. If g(W) does not lie in Ω then the image of a small ball about W must contain points with in Ω with arbitrarily large operator norm. Precomposing g with a suitable element in G, it follows that Z = g(0) will have operator norm greater than 1. If g(W) already lies in Ω, it will also have operator norm greater than 1 and W can be then be taken to be 0 by precomposing with a suitable element of G.

Pre-composing g with a scaling transformation and post-composing g with a unitary transformation, it can be assumed that g(0) is a diagonal matrix with entries λ_i ≥ 0 with r = λ₁ > 0 and that the image of the unit ball is contained in a small ball around this point. The entries λ_i with i ≥ 2 can be separately scaled byelements of the Olshanki semigroup so that λ_i < 1; and then they can be sent to 0 by elements of G lying in commuting copies of SU(1,1). So g(0) is a diagonal matrix with entries r, 0,...,0, where r > 1.

Notes

↑
See:
- Vinberg 1980
- Paneitz 1983
↑
See:
- Howe 1988
- Folland 1989
↑
See:
- Olshanskii 1981
- Hilgert & Neeb 1993, pp. 197–199
↑ Hervé 1963, pp. 83–84
↑ Hervé 1963, pp. 83–84
↑
See:
- Lawson 1998
- Hilgert & Neeb 1993, pp. 48–56
↑
See:
- Lawson 1998
- Hilgert & Neeb 1993, pp. 48–56
↑ See for example Siegel 1932, pp. 12, 14–15
↑ Mok 1989, pp. 65–71

References

Folland, G. B. (1989), Harmonic analysis in phase space, Annals of Mathematics Studies 122, Princeton University Press, ISBN 9780691085289
Hervé, M. (1963), Several complex variables. Local theory, Tata Institute of Fundamental Research
Hilgert, Joachim; Hofmann, Karl Heinrich; Lawson, Jimmie D. (1989), Lie groups, convex cones, and semigroups, Oxford Mathematical Monographs, Oxford University Press, ISBN 0-19-853569-4
Hilgert, Joachim; Neeb, Karl-Hermann (1993), Lie semigroups and their applications, Lecture Notes in Mathematics 1552, Springer-Verlag, ISBN 3540569545
Howe, R. (1988), "The Oscillator Semigroup", Proceedings of Symposia in Pure Mathematics (American Mathematical Society) 48: 61–132, doi:10.1090/pspum/048/974332
Kumaresan, S.; Ranjan, A. (1982), "On invariant convex cones in simple Lie algebras", Proc. Indian Acad. Sci. Math. Sci. 91: 167–182, doi:10.1007/bf02881028
Lawson, J. D. (1994), "Maximal Olshanski semigroups", Journal of Lie Theory 4: 17–29
Lawson, J. D. (1998), "Semigroups in Möbius and Lorentzian geometry", Geom. Dedicata 70: 139–180
Mok, Ngaiming (1989), Metric Rigidity Theorems on Hermitian Locally Symmetric Manifolds, World Scientific, ISBN 9971-5-0802-8
Olshanskii, G. I. (1981), "Invariant cones in Lie algebras, Lie semigroups and the holomorphic discrete series", Funct. Anal. Appl. 15: 275–285, doi:10.1007/bf01106156
Paneitz, Stephen M. (1981), "Invariant convex cones and causality in semisimple Lie algebras and groups", J. Funct. Anal., 313–359