Interval order
In mathematics, especially order theory,
the interval order for a collection of intervals on the real line
is the partial order corresponding to their left-to-right precedence relation—one interval, I1, being considered less than another, I2, if I1 is completely to the left of I2.
More formally, a poset 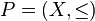 is an interval order if and only if
there exists a bijection from
is an interval order if and only if
there exists a bijection from  to a set of real intervals,
so
to a set of real intervals,
so 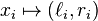 ,
such that for any
,
such that for any 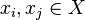 we have
we have
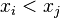 in
in  exactly when
exactly when 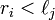 .
Such posets may be equivalently
characterized as those with no induced subposet isomorphic to the
pair of two element chains, the
.
Such posets may be equivalently
characterized as those with no induced subposet isomorphic to the
pair of two element chains, the 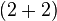 free posets
.[1]
free posets
.[1]
The subclass of interval orders obtained by restricting the intervals to those of unit length, so they all have the form 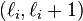 , is precisely the semiorders.
, is precisely the semiorders.
The complement of the comparability graph of an interval order ( , ≤)
is the interval graph
, ≤)
is the interval graph 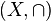 .
.
Interval orders should not be confused with the interval-containment orders, which are the containment orders on intervals on the real line (equivalently, the orders of dimension ≤ 2).
Interval dimension
The interval dimension of a partial order can be defined as the minimal number of interval order extensions realizing this order, in a similar way to the definition of the order dimension which uses linear extensions. The interval dimension of an order is always less than its order dimension,[2] but interval orders with high dimensions are known to exist. While the problem of determining the order dimension of general partial orders is known to be NP-complete, the complexity of determining the order dimension of an interval order is unknown.[3]
Combinatorics
In addition to being isomorphic to 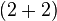 free posets,
unlabeled interval orders on
free posets,
unlabeled interval orders on ![[n]](../I/m/de504dafb2a07922de5e25813d0aaafd.png) are also in bijection
with a subset of fixed point free involutions
on ordered sets with cardinality
are also in bijection
with a subset of fixed point free involutions
on ordered sets with cardinality 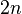 .[4] These are the
involutions with no left or right neighbor nestings where, for
.[4] These are the
involutions with no left or right neighbor nestings where, for
 an involution on
an involution on ![[2n]](../I/m/ddc77784e6b290ae1340bfa48d6b9a9c.png) , a left nesting is
an
, a left nesting is
an ![i \in [2n]](../I/m/7c04db5022bbca4c4e99aad1753458af.png) such that
such that 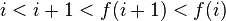 and a right nesting is an
and a right nesting is an ![i \in [2n]](../I/m/7c04db5022bbca4c4e99aad1753458af.png) such that
such that
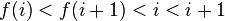 .
.
Such involutions, according to semi-length, have ordinary generating function [5]
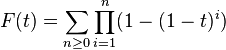 .
.
Hence the number of unlabeled interval orders of size  is given by the coefficient of
is given by the coefficient of 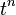 in the expansion of
in the expansion of
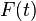 .
.
1, 2, 5, 15, 53, 217, 1014, 5335, 31240, 201608, 1422074, 10886503, 89903100, 796713190, 7541889195, 75955177642, … (sequence A022493 in OEIS)
Notes
References
- Bousquet-Mélou, Mireille; Claesson, Anders; Dukes, Mark; Kitaev, Sergey (2010), "(2+2) free Posets, Ascent Sequences and Pattern Avoiding Permutations", J. Comb. Theory Ser. A (Academic Press, Inc.) 117 (7): 884–909, doi:10.1016/j.jcta.2009.12.007, ISSN 0097-3165
- Zagier, Don (2001), "Vassiliev invariants and a strange identity related to the Dedekind eta-function", Topology 40 (5): 945–960, doi:10.1016/s0040-9383(00)00005-7, ISSN 0040-9383
- Fishburn, Peter (1985), Interval Orders and Interval Graphs: A Study of Partially Ordered Sets, John Wiley
- Fishburn, Peter C. (1970), "Intransitive indifference with unequal indifference intervals", Journal of Mathematical Psychology 7 (1): 144–149, doi:10.1016/0022-2496(70)90062-3.
- Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7.