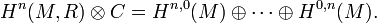Intermediate Jacobian

In mathematics, the intermediate Jacobian of a compact Kähler manifold or Hodge structure is a complex torus that is a common generalization of the Jacobian variety of a curve and the Picard variety and the Albanese variety. It is obtained by putting a complex structure on the torus Hn(M,R)/Hn(M,Z) for n odd. There are several different natural ways to put a complex structure on this torus, giving several different sorts of intermediate Jacobians, including one due to Weil (1952) and one due to Griffiths (1968, 1968b). The ones constructed by Weil have natural polarizations if M is projective, and so are abelian varieties, while the ones constructed by Griffiths behave well under holomorphic deformations.

A complex structure on a real vector space is given by an automorphism I with square −1. The complex structures on Hn(M,R) are defined using the Hodge decomposition

H^{n}(M,{ R}) \otimes { C} = H^{n,0}(M)\oplus\cdots\oplus H^{0,n}(M). \,

On Hp,q the Weil complex structure IW is multiplication by ip−q, while the Griffiths complex structure IG is multiplication by i if p > q and −i if p < q. Both these complex structures map Hn(M,R) into itself and so defined complex structures on it.

For n = 1 the intermediate Jacobian is the Picard variety, and for n = 2 dim(M) − 1 it is the Albanese variety. In these two extreme cases the constructions of Weil and Griffiths are equivalent.

Clemens & Griffiths (1972) used intermediate Jacobians to show that non-singular cubic threefolds are not rational, even though they are unirational.

References