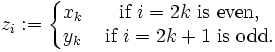Interleave sequence
In mathematics, an interleave sequence is obtained by merging or shuffling two sequences.
Let  be a set, and let
be a set, and let 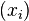 and
and 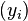 ,
, 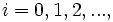 be two sequences in
be two sequences in  The interleave sequence is defined to be the sequence
The interleave sequence is defined to be the sequence 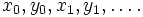 Formally, it is the sequence
Formally, it is the sequence 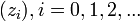 given by
given by
Properties
- The interleave sequence
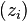 is convergent if and only if the sequences
is convergent if and only if the sequences 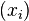 and
and 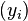 are convergent and have the same limit.[1]
are convergent and have the same limit.[1]
- Consider two real numbers a and b greater than zero and smaller than 1. One can interleave the sequences of digits of a and b, which will determine a third number c, also greater than zero and smaller than 1. In this way one obtains an injection from the square (0, 1)×(0, 1) to the interval (0, 1). Different radixes give rise to different injections; the one for the binary numbers is called the Z-order curve or Morton code.[2]
References
- ↑ Strichartz, Robert S. (2000), The Way of Analysis, Jones & Bartlett Learning, p. 78, ISBN 9780763714970.
- ↑ Mamoulis, Nikos (2012), Spatial Data Management, Synthesis lectures on data management 21, Morgan & Claypool Publishers, pp. 22–23, ISBN 9781608458325.
This article incorporates material from Interleave sequence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.