Interdependent networks
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
|
||||
The study of interdependent networks is a subfield of network science dealing with phenomena caused by the interactions between complex networks. Though there may be a wide variety of interactions between networks, dependency focuses on the scenario in which the nodes in one network require support from nodes in another network.[1][2][3][4] [5] [6]
Motivation for the model
In nature, networks rarely appear in isolation. They are typically elements in larger systems and can have non-trivial effects on one and other. For example, infrastructure networks exhibit interdependency to a large degree. The power stations which form the nodes of the power grid require fuel delivered via a network of roads or pipes and are also controlled via the nodes of communications network. Though the transportation network does not depend on the power network to function, the communications network does. Thus the deactivation of a critical number of nodes in either the power network or the communication network can lead to a series of cascading failures across the system with potentially catastrophic repercussions. If the two networks were treated in isolation, this important feedback effect would not be seen and predictions of network robustness would be greatly overestimated.
Dependency links
Links in a standard network represent connectivity, providing information about how one node can be reached from another. Dependency links represent a need for support from one node to another. This relationship is often, though not necessarily, mutual and thus the links can be directed or undirected. Crucially, a node loses its ability to function as soon as the node it is dependent on ceases to function while it may not be so severely effected by losing a node it is connected to.
In percolation theory, a node is considered active as long as it is connected to the giant component. The introduction of dependency links adds another condition: that the node that it depends on is also active.
Dependency can be defined between different networks[1] and also within the same network.[7]
Percolation properties and phase transitions
Interdependent networks have markedly different percolation properties than single-networks.
If a single network is subjected to random attack  , the largest connected component decreases continuously with a divergence of its derivative
, the largest connected component decreases continuously with a divergence of its derivative 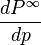 at the percolation threshold
at the percolation threshold 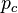 , a second-order phase transition. This result is established for ER networks, lattices and other standard topologies.
, a second-order phase transition. This result is established for ER networks, lattices and other standard topologies.
However, when multiple networks are interdependent, cascading failures emerge due to the positive feedback caused by dependency links. This family of processes causes a discontinuous or first order phase transition. This has been observed for random networks as well as lattices.[7] Furthermore, for embedded interdependent networks the transition is particularly precipitous without even a critical exponent for 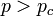 .[8]
.[8]
Surprisingly, it has been shown that—contrary to the results for single networks—interdependent random networks with broader degree distributions are more vulnerable than those with narrow degree distributions. The high degree which is an asset in single networks can be a liability in interdependent networks. This is because the hubs which increase the robustness in single networks can be dependent on vulnerable low-degree nodes. The removal of the low-degree node then removes the hub and all of its links.[1][3]
Dynamics of cascading failure
A typical cascading failure in a system of interdependent networks can be described as follows:[1] We take two networks  and
and  with
with  nodes and a given topology . Each node
nodes and a given topology . Each node 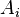 in
in  relies on a critical resource provided by a node
relies on a critical resource provided by a node 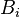 in
in  and vice versa. If
and vice versa. If 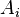 stops functioning,
stops functioning, 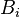 will also stop functioning and vice versa. The failure is triggered by the removal of a fraction
will also stop functioning and vice versa. The failure is triggered by the removal of a fraction  of nodes from
of nodes from  along with the links in
along with the links in  which were attached to each of those nodes. Since every node in
which were attached to each of those nodes. Since every node in  depends on a node in
depends on a node in  , this causes the removal of the same fraction
, this causes the removal of the same fraction  of nodes in
of nodes in  . In network theory, we assume that only nodes which are a part of the largest connected component can continue to function. Since the arrangement of links in
. In network theory, we assume that only nodes which are a part of the largest connected component can continue to function. Since the arrangement of links in  and
and  are different, they fragment into different sets of connected components. The smaller components in
are different, they fragment into different sets of connected components. The smaller components in  cease to function and when they do, they cause the same number of nodes (but in different locations) in
cease to function and when they do, they cause the same number of nodes (but in different locations) in  to cease to function as well. This process continues iteratively between the two networks until no more nodes are removed. This process leads to a percolation phase transition at a value
to cease to function as well. This process continues iteratively between the two networks until no more nodes are removed. This process leads to a percolation phase transition at a value 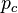 which is substantially larger than the value obtained for a single network.
which is substantially larger than the value obtained for a single network.
Effect of network topology
In interdependent random networks in which a fraction  of the nodes in one network are dependent on another, it is found that there is a critical value
of the nodes in one network are dependent on another, it is found that there is a critical value 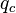 above which first-order phase transitions are possible.
above which first-order phase transitions are possible.
In spatially embedded interdependent networks, a new kind of failure has been observed in which a relatively small failure can propagate through space and destroy an entire system of networks.[8]
Comparison to many-particle systems in physics
In statistical physics, phase transitions can only appear in many particle systems. Though phase transitions are well known in network science, in single networks they are second order only. With the introduction of internetwork dependency, first order transitions emerge. This is a new phenomenon and one with profound implications for systems engineering. Where system dissolution takes place after steady (if steep) degradation for second order transitions, the existence of a first order transition implies that the system can go from a relatively healthy state to complete collapse with no advance warning.
Examples of interdependent networks
- Infrastructure networks The network of power stations depends on instructions from the communications network which require power themselves.[9]
- Transportation networks The networks of airports and seaports are interdependent in that in a given city, the ability of that city's airport to function is dependent upon resources obtained from the seaport or vice versa.[10][11]
- Physiological networks The nervous and cardiovascular system are each composed of many connected parts which can be represented as a network. In order to function, they require connectivity within their own network as well as resources available only from the other network.[12]
- Economic/financial networks Availability of credit from the banking network and economic production by the network of commercial firms are interdependent. A bipartite network model of banks and bank assets has recently been used to examine failure propagation in the economy at large.[13]
- Protein networks A biological process regulated by a number of proteins is often represented as a network. Since the same proteins participate in different processes, the networks are interdependent.
- Ecological networks Food webs constructed from species which depend on one and other are interdependent when the same species participates in different webs.[14]
- Climate networks Spatial measurements of different climatological variables define a network. The networks defined by different sets of variables are interdependent.[15]
See also
- Cascading failure
- 2003 Italy blackout
- Complex networks
- Percolation theory
References
- ↑ 1.0 1.1 1.2 1.3 Buldyrev, Sergey V.; Parshani, Roni; Paul, Gerald; Stanley, H. Eugene; Havlin, Shlomo (2010). "Catastrophic cascade of failures in interdependent networks". Nature 464 (7291): 1025–1028. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. ISSN 0028-0836. PMID 20393559.
- ↑ Vespignani, Alessandro (2010). "Complex networks: The fragility of interdependency". Nature 464 (7291): 984–985. doi:10.1038/464984a. ISSN 0028-0836. PMID 20393545.
- ↑ 3.0 3.1 Gao, Jianxi; Buldyrev, Sergey V.; Stanley, H. Eugene; Havlin, Shlomo (2011). "Networks formed from interdependent networks". Nature Physics 8 (1): 40–48. doi:10.1038/nphys2180. ISSN 1745-2473.
- ↑ Kenett, Dror Y.; Gao, Jianxi; Huang, Xuqing; Shao, Shuai; Vodenska, Irena; Buldyrev, Sergey V.; Paul, Gerald; Stanley, H. Eugene; Havlin, Shlomo (2014). "Network of Interdependent Networks: Overview of Theory and Applications". In D'Agostino, Gregorio; Scala, Antonio. Networks of Networks: The Last Frontier of Complexity. Understanding Complex Systems. Springer International Publishing. pp. 3–36. doi:10.1007/978-3-319-03518-5_1. ISBN 978-3-319-03517-8.
- ↑ Danziger, Michael M.; Bashan, Amir; Berezin, Yehiel; Shekhtman, Louis M.; Havlin, Shlomo (2014). "An Introduction to Interdependent Networks". 22nd International Conference, NDES 2014, Albena, Bulgaria, July 4-6, 2014. Proceedings 438: 189–202. doi:10.1007/978-3-319-08672-9_24. Retrieved 8 March 2015.
- ↑ Kivelä, Mikko; Arenas, Alex; Barthelemy, Marc; Gleeson, James P.; Moreno, Yamir; Porter, Mason A. (2014). "Multilayer networks". Journal of Complex Networks 2 (3): 203–271. doi:10.1093/comnet/cnu016. Retrieved 8 March 2015.
- ↑ 7.0 7.1 Parshani, R.; Buldyrev, S. V.; Havlin, S. (2010). "Critical effect of dependency groups on the function of networks". Proceedings of the National Academy of Sciences 108 (3): 1007–1010. Bibcode:2011PNAS..108.1007P. doi:10.1073/pnas.1008404108. ISSN 0027-8424.
- ↑ 8.0 8.1 Li, Wei; Bashan, Amir; Buldyrev, Sergey V.; Stanley, H. Eugene; Havlin, Shlomo (2012). "Cascading Failures in Interdependent Lattice Networks: The Critical Role of the Length of Dependency Links". Physical Review Letters 108 (22): 228702. Bibcode:2012PhRvL.108v8702L. doi:10.1103/PhysRevLett.108.228702. ISSN 0031-9007. PMID 23003664.
- ↑ Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. (2001). "Identifying, understanding, and analyzing critical infrastructure interdependencies". IEEE Control Systems Magazine 21 (6): 11–25. doi:10.1109/37.969131. ISSN 0272-1708.
- ↑ Parshani, R.; Rozenblat, C.; Ietri, D.; Ducruet, C.; Havlin, S. (2010). "Inter-similarity between coupled networks". EPL (Europhysics Letters) 92 (6): 68002. doi:10.1209/0295-5075/92/68002. ISSN 0295-5075.
- ↑ Gu, Chang-Gui; Zou, Sheng-Rong; Xu, Xiu-Lian; Qu, Yan-Qing; Jiang, Yu-Mei; He, Da Ren; Liu, Hong-Kun; Zhou, Tao (2011). "Onset of cooperation between layered networks". Physical Review E 84 (2). doi:10.1103/PhysRevE.84.026101. ISSN 1539-3755.
- ↑ Bashan, Amir; Bartsch, Ronny P.; Kantelhardt, Jan. W.; Havlin, Shlomo; Ivanov, Plamen Ch. (2012). "Network physiology reveals relations between network topology and physiological function". Nature Communications 3: 702. doi:10.1038/ncomms1705. ISSN 2041-1723. PMC 3518900. PMID 22426223.
- ↑ Huang, Xuqing; Vodenska, Irena; Havlin, Shlomo; Stanley, H. Eugene (2013). "Cascading Failures in Bi-partite Graphs: Model for Systemic Risk Propagation". Scientific Reports 3. doi:10.1038/srep01219. ISSN 2045-2322.
- ↑ Pocock, M. J. O.; Evans, D. M.; Memmott, J. (2012). "The Robustness and Restoration of a Network of Ecological Networks". Science 335 (6071): 973–977. doi:10.1126/science.1214915. ISSN 0036-8075. PMID 22363009.
- ↑ Donges, J. F.; Schultz, H. C. H.; Marwan, N.; Zou, Y.; Kurths, J. (2011). "Investigating the topology of interacting networks". The European Physical Journal B 84 (4): 635–651. doi:10.1140/epjb/e2011-10795-8. ISSN 1434-6028.