Interacting particle system

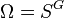In probability theory, an interacting particle system (IPS) is a stochastic process (X(t))_{t \in \mathbb R^+} on some configuration space \Omega= S^G given by a site space, a countable-infinite graph G and a local state space, a compact metric space S . More precisely IPS are continuous-time Markov jump processes describing the collective behavior of stochastically interacting components. IPS are the continuous-time analogue of stochastic cellular automata. Among the main examples are the voter model, the contact process, the asymmetric simple exclusion process (ASEP), the Glauber dynamics and in particular the stochastic Ising model.

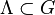IPS are usually defined via their Markov generator giving rise to a unique Markov process using Markov semigroups and the Hille-Yosida theorem. The generator again is given via so-called transition rates c_\Lambda(\eta,\xi)>0 where \Lambda\subset G is a finite set of sites and 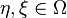\eta,\xi\in\Omega with \eta_i=\xi_i for all i\notin\Lambda. 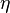The rates describe exponential waiting times of the process to jump from configuration \eta into configuration 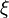\xi. More generally the transition rates are given in form of a finite measure c_\Lambda(\eta,d\xi) on S^\Lambda. The generator L of an IPS has the following form: Let f be an observable in the domain of L which is a subset of the real valued continuous function on the configuration space, then

Lf(\eta)=\sum_\Lambda\int_{\xi:\xi_{\Lambda^c}=\eta_{\Lambda^c}}c_\Lambda(\eta,d\xi)[f(\xi)-f(\eta)].

For example for the stochastic Ising model we have 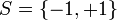G=\mathbb Z^d, S=\{-1,+1\}, c_\Lambda=0 if \Lambda\neq\{i\} for some i\in G and

c_i(\eta,\eta^i)=\exp[-\beta\sum_{j:|j-i|=1}\eta_i\eta_j]

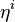where \eta^i is the configuration equal to 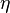\eta except it is flipped at site i. \beta is a new parameter modeling the inverse temperature.

References