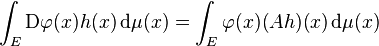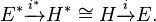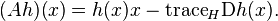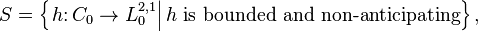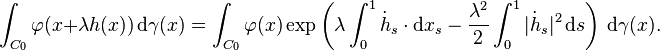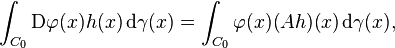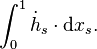Integration by parts operator
In mathematics, an integration by parts operator is a linear operator used to formulate integration by parts formulae; the most interesting examples of integration by parts operators occur in infinite-dimensional settings and find uses in stochastic analysis and its applications.
Definition
Let E be a Banach space such that both E and its continuous dual space E∗ are separable spaces; let μ be a Borel measure on E. Let S be any (fixed) subset of the class of functions defined on E. A linear operator A : S → L2(E, μ; R) is said to be an integration by parts operator for μ if
for every C1 function φ : E → R and all h ∈ S for which either side of the above equality makes sense. In the above, Dφ(x) denotes the Fréchet derivative of φ at x.
Examples
- Consider an abstract Wiener space i : H → E with abstract Wiener measure γ. Take S to be the set of all C1 functions from E into E∗; E∗ can be thought of as a subspace of E in view of the inclusions
- For h ∈ S, define Ah by
- This operator A is an integration by parts operator, also known as the divergence operator; a proof can be found in Elworthy (1974).
- The classical Wiener space C0 of continuous paths in Rn starting at zero and defined on the unit interval [0, 1] has another integration by parts operator. Let S be the collection
- i.e., all bounded, adapted processes with absolutely continuous sample paths. Let φ : C0 → R be any C1 function such that both φ and Dφ are bounded. For h ∈ S and λ ∈ R, the Girsanov theorem implies that
- Differentiating with respect to λ and setting λ = 0 gives
- where (Ah)(x) is the Itō integral
- The same relation holds for more general φ by an approximation argument; thus, the Itō integral is an integration by parts operator and can be seen as an infinite-dimensional divergence operator. This is the same result as the integration by parts formula derived from the Clark-Ocone theorem.
References
- Bell, Denis R. (2006). The Malliavin calculus. Mineola, NY: Dover Publications Inc. pp. x+113. ISBN 0-486-44994-7. MR 2250060 (See section 5.3)
- Elworthy, K. David (1974). "Gaussian measures on Banach spaces and manifolds". Global analysis and its applications (Lectures, Internat. Sem. Course, Internat. Centre Theoret. Phys., Trieste, 1972), Vol. II. Vienna: Internat. Atomic Energy Agency. pp. 151–166. MR 0464297