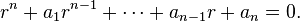Integral closure of an ideal

In algebra, the integral closure of an ideal I of a commutative ring R, denoted by 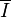$\overline{I}$ , is the set of all elements r in R that are integral over I: there exist 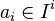$a_i \in I^i$ such that

r^n + a_1 r^{n-1} + \cdots + a_{n-1} r + a_n = 0.

It is similar to the integral closure of a subring. For example, if R is a domain, an element r in R belongs to 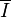$\overline{I}$ if and only if there is a finitely generated R-module M, annihilated only by zero, such that 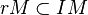$r M \subset I M$ . 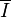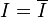It follows that $\overline{I}$ is an ideal of R (in fact, the integral closure of an ideal is always an ideal; see below.) I is said to be integrally closed if $I = \overline{I}$ .

The integral closure of an ideal appears in a theorem of Rees that characterizes an analytically unramified ring.

Examples

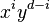In $\mathbb{C}[x, y]$ , $x^i y^{d-i}$ is integral over $(x^d, y^d)$ .
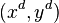Radical ideals (e.g., prime ideals) are integrally closed. The intersection of integrally closed ideals is integrally closed.
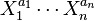Let $R = k[X_1, \ldots, X_n]$ be a polynomial ring over a field k. An ideal I in R is called monomial if it is generated by monomials; i.e., $X_1^{a_1} \cdots X_n^{a_n}$ . The integral closure of a monomial ideal is monomial.

Structure results

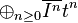Let R be a ring. The Rees algebra $R[It] = \oplus_{n \ge 0} I^n t^n$ can be used to compute the integral closure of an ideal. The structure result is the following: the integral closure of $R[It]$ in $R[t]$ , which is graded, is $\oplus_{n \ge 0} \overline{I^n} t^n$ . In particular, 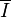$\overline{I}$ is an ideal and 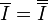$\overline{I} = \overline{\overline{I}}$ ; i.e., the integral closure of an ideal is integrally closed. It also follows that the integral closure of a homogeneous ideal is homogeneous.

The following type of results is called the Briancon–Skoda theorem: let R be a regular ring and $I$ an ideal generated by $l$ elements. Then 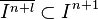$\overline{I^{n+l}} \subset I^{n+1}$ for any $n \ge 0$ .

A theorem of Rees states: let (R, m) be a noetherian local ring. Assume it is formally equidimensional (i.e., the completion is equidimensional.). Then two m-primary ideals 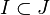$I \subset J$ have the same integral closure if and only if they have the same multiplicity.^[1]

Notes

↑ Swanson 2006, Theorem 11.3.1

References

Eisenbud, David, Commutative Algebra with a View Toward Algebraic Geometry, Graduate Texts in Mathematics, 150, Springer-Verlag, 1995, ISBN 0-387-94268-8.
Huneke, Craig; Swanson, Irena (2006), Integral closure of ideals, rings, and modules, London Mathematical Society Lecture Note Series 336, Cambridge, UK: Cambridge University Press, ISBN 978-0-521-68860-4, MR 2266432

Integral closure of an ideal

Examples

Structure results

Notes

References

Further reading