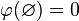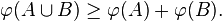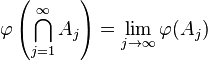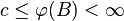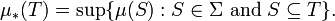Inner measure

In mathematics, in particular in measure theory, an inner measure is a function on the set of all subsets of a given set, with values in the extended real numbers, satisfying some technical conditions. Intuitively, the inner measure of a set is a lower bound of the size of that set.

Definition

An inner measure is a function

\varphi: 2^X \rightarrow [0, \infty],

defined on all subsets of a set X, that satisfies the following conditions:

Null empty set: The empty set has zero inner measure (see also: measure zero).

\varphi(\varnothing) = 0

Superadditive: For any disjoint sets A and B,

\varphi( A \cup B) \geq \varphi(A) + \varphi( B ).

Limits of decreasing towers: For any sequence {A_j} of sets such that 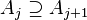$A_j \supseteq A_{j+1}$ for each j and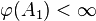 $\varphi(A_1) < \infty$

\varphi \left(\bigcap_{j=1}^\infty A_j\right) = \lim_{j \to \infty} \varphi(A_j)

Infinity must be approached: If 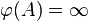$\varphi(A) = \infty$ for a set A then for every positive number c, there exists a B which is a subset of A such that,

c \leq \varphi( B) <\infty

The inner measure induced by a measure

Let Σ be a σ-algebra over a set X and μ be a measure on Σ. Then the inner measure μ_* induced by μ is defined by

\mu_*(T)=\sup\{\mu(S):S\in\Sigma\text{ and }S\subseteq T\}.

Essentially μ_* gives a lower bound of the size of any set by ensuring it is at least as big as the μ-measure of any of its Σ-measurable subsets. Even though the set function μ_* is usually not a measure, μ_* shares the following properties with measures:

μ_*(∅)=0,
μ_* is non-negative,
If E ⊆ F then μ_*(E) ≤ μ_*(F).

Measure completion

Main article: complete measure

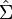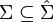Induced inner measures are often used in combination with outer measures to extend a measure to a larger σ-algebra. If μ is a finite measure defined on a σ-algebra Σ over X and μ* and μ_* are corresponding induced outer and inner measures, then the sets T ∈ 2^X such that μ_*(T) = μ*(T) form a σ-algebra $\hat \Sigma$ with $\Sigma\subseteq\hat\Sigma$ .^[1] The set function μ̂ defined by

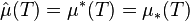\hat\mu(T)=\mu^*(T)=\mu_*(T)

for all 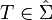$T \in \hat \Sigma$ is a measure on 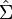$\hat \Sigma$ known as the completion of μ.

References

↑ Halmos 1950, § 14, Theorem F

Halmos, Paul R., Measure Theory, D. Van Nostrand Company, Inc., 1950, pp. 58.
A. N. Kolmogorov & S. V. Fomin, translated by Richard A. Silverman, Introductory Real Analysis, Dover Publications, New York, 1970, ISBN 0-486-61226-0 (Chapter 7)