Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories. The dual notion is that of a projective object.
General Definition
Let 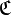 be a category and let
be a category and let  be a class of morphisms of
be a class of morphisms of 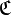 .
.
An object 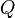 of
of 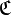 is said to be
is said to be  -injective if for every morphism
-injective if for every morphism  and every morphism
and every morphism 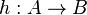 in
in  there exists a morphism
there exists a morphism  extending (the domain of)
extending (the domain of)  , i.e.
, i.e. 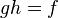 . In other words,
. In other words,  is injective iff any
is injective iff any  -morphism into
-morphism into 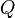 extends (via composition on the left) to a morphism into
extends (via composition on the left) to a morphism into 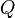 .
.
The morphism  in the above definition is not required to be uniquely determined by
in the above definition is not required to be uniquely determined by 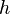 and
and  .
.
In a locally small category, it is equivalent to require that the hom functor 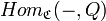 carries
carries  -morphisms to epimorphisms (surjections).
-morphisms to epimorphisms (surjections).
The classical choice for  is the class of monomorphisms, in this case, the expression injective object is used.
is the class of monomorphisms, in this case, the expression injective object is used.
Abelian case
If 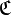 is an abelian category, an object A of
is an abelian category, an object A of 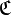 is injective iff its hom functor HomC(–,A) is exact.
is injective iff its hom functor HomC(–,A) is exact.
The abelian case was the original framework for the notion of injectivity.
Enough injectives
Let 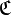 be a category, H a class of morphisms of
be a category, H a class of morphisms of 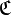 ; the category
; the category 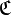 is said to have enough H-injectives if for every object X of
is said to have enough H-injectives if for every object X of 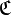 , there exist a H-morphism from X to an H-injective object.
, there exist a H-morphism from X to an H-injective object.
Injective hull
A H-morphism g in 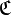 is called H-essential if for any morphism f, the composite fg is in H only if f is in H.
is called H-essential if for any morphism f, the composite fg is in H only if f is in H.
If f is a H-essential H-morphism with a domain X and an H-injective codomain G, G is called an H-injective hull of X. This H-injective hull is then unique up to a noncanonical isomorphism.
Examples
- In the category of Abelian groups and group homomorphisms, an injective object is a divisible group.
- In the category of modules and module homomorphisms, R-Mod, an injective object is an injective module. R-Mod has injective hulls (as a consequence, R-Mod has enough injectives).
- In the category of metric spaces and nonexpansive mappings, Met, an injective object is an injective metric space, and the injective hull of a metric space is its tight span.
- In the category of T0 spaces and continuous mappings, an injective object is always a Scott topology on a continuous lattice therefore it is always sober and locally compact.
- In the category of simplicial sets, the injective objects with respect to the class of anodyne extensions are Kan complexes.
- In the category of partially ordered sets and monotonic functions between posets, the complete lattices form the injective objects for order-embeddings, and the Dedekind–MacNeille completion of a partially ordered set is its injective hull.
- One also talks about injective objects in more general categories, for instance in functor categories or in categories of sheaves of OX modules over some ringed space (X,OX).
References
- J. Rosicky, Injectivity and accessible categories
- F. Cagliari and S. Montovani, T0-reflection and injective hulls of fibre spaces