Initial mass function
| Star formation |
|---|
 |
| Object classes |
|
Interstellar medium Molecular cloud Bok globule Dark nebula Young stellar object Protostar T Tauri star Pre–main-sequence star Herbig Ae/Be star Herbig–Haro object |
| Theoretical concepts |
|
Initial mass function Jeans instability Kelvin–Helmholtz mechanism Nebular hypothesis Planetary migration |
|
|
In astronomy, the initial mass function (IMF) is an empirical function that describes the distribution of initial masses for a population of stars. The IMF is often given as a probability distribution function (PDF) for the mass at which a star enters the main sequence (begins hydrogen fusion). The distribution function can then be used to construct the mass distribution (the histogram of stellar masses) of a population of stars. The properties and evolution of a star are closely related to its mass, so the IMF is an important diagnostic tool for astronomers studying large quantities of stars. For example, the initial mass of a star is the primary factor determining its colour, luminosity, and lifetime. The IMF is relatively invariant from one group of stars to another, though some observations suggest that the IMF is different in different environments.[1]
Form of the IMF
The IMF is often stated in terms of a series of power laws, where 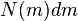 (sometimes also represented as
(sometimes also represented as 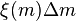 ), the number of stars with masses in the range
), the number of stars with masses in the range  to
to 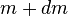 within a specified volume of space, is proportional to
within a specified volume of space, is proportional to 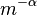 , where
, where  is a dimensionless exponent. The IMF can be inferred from the present day stellar luminosity function by using the stellar mass-luminosity relation together with a model of how the star formation rate varies with time. Commonly used forms of the IMF are the Kroupa (2001) broken power law[2] and the Chabrier (2003) log-normal.[3]
is a dimensionless exponent. The IMF can be inferred from the present day stellar luminosity function by using the stellar mass-luminosity relation together with a model of how the star formation rate varies with time. Commonly used forms of the IMF are the Kroupa (2001) broken power law[2] and the Chabrier (2003) log-normal.[3]
Salpeter (1955)
The IMF of stars more massive than our sun was first quantified by Edwin Salpeter in 1955.[4] His work favoured an exponent of 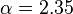 . This form of the IMF is called the Salpeter function or a Salpeter IMF. It shows that the number of stars in each mass range decreases rapidly with increasing mass. The Salpeter Initial Mass Function is
. This form of the IMF is called the Salpeter function or a Salpeter IMF. It shows that the number of stars in each mass range decreases rapidly with increasing mass. The Salpeter Initial Mass Function is
Miller-Scalo (1979)
Later authors extended the work below one solar mass (M☉). Glenn E. Miller and John M. Scalo suggested that the IMF "flattened" (approached 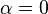 ) below one solar mass.[5]
) below one solar mass.[5]
Chabrier (2003)
Chabrier 2003 for individual stars:
![\xi (m) \Delta m= 0.158 (1/m) \exp[- (\log(m)-\log(0.08))^2/(2 \times 0.69^2)]](../I/m/1977cb23dd4743ace40d2602c83f45c2.png) for
for 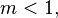
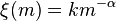 for
for 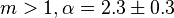
Chabrier 2003 for stellar systems:
![\xi (m) \Delta m= 0.086 (1/m) \exp[- (\log(m)-\log(0.22))^2/(2 \times 0.57^2)]](../I/m/f215d05c6b3d87e2e740ca6d2bfa97c1.png) for
for 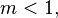
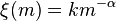 for
for 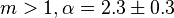
Kroupa (2001)
Pavel Kroupa kept 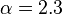 above half a solar mass, but introduced
above half a solar mass, but introduced 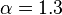 between 0.08-0.5 M☉ and
between 0.08-0.5 M☉ and 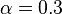 below 0.08 M☉.
below 0.08 M☉.
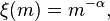
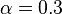 for
for 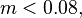
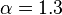 for
for 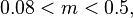
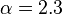 for
for 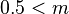
Uncertainties
There are large uncertainties concerning the substellar region. In particular, the classical assumption of a single IMF covering the whole substellar and stellar mass range is being questioned in favour of a two-component IMF to account for possible different formation modes of substellar objects. I.e. one IMF covering brown dwarfs and very-low-mass stars on the one hand, and another ranging from the higher-mass brown dwarfs to the most massive stars on the other. Note that this leads to an overlap region between about 0.05 and 0.2 M☉ where both formation modes may account for bodies in this mass range.[6]
Further reading
- John Scalo, The initial mass function of massive stars in galaxies. Empirical evidence, Luminous stars and associations in galaxies; Proceedings of the Symposium, Porto-Kheli, Greece, May 26–31, 1985. Dordrecht, D. Reidel Publishing Co., 1986, p. 451-466.
- John Scalo, The Stellar Initial Mass Function, Fundamentals of cosmic physics, vol 11 pp. 1–278, University of Texas (1986).
- Pavel Kroupa, The initial mass function of stars: evidence for uniformity in variable systems, Science 295, 82 (2002)
- John Gallagher & Linda Sparke, Galaxies in the Universe, Cambridge Press, 66 (2007)
References
- ↑ http://adsabs.harvard.edu/abs/2013ApJ...771...29G
- ↑ Kroupa, Pavel (2001). "On the variation of the initial mass function". MNRAS 322: 231. arXiv:astro-ph/0009005. Bibcode:2001MNRAS.322..231K. doi:10.1046/j.1365-8711.2001.04022.x.
- ↑ Chabrier, Gilles (2003). "Galactic stellar and substellar initial mass function". PASP 115: 763. arXiv:astro-ph/0304382. Bibcode:2003PASP..115..763C. doi:10.1086/376392.
- ↑ Salpeter, Edwin (1955). "The luminosity function and stellar evolution". ApJ 121: 161. Bibcode:1955ApJ...121..161S. doi:10.1086/145971.
- ↑ Miller, Glenn; Scalo, John (1979). "The initial mass function and stellar birthrate in the solar neighborhood". ApJS 41: 513. Bibcode:1979ApJS...41..513M. doi:10.1086/190629.
- ↑ Kroupa, Pavel et al. (2012). "The stellar and sub-stellar IMF of simple and composite populations". Stellar Systems and Galactic Structure, Vol. V.