Infrared fixed point

In physics, an infrared fixed point is a set of coupling constants, or other parameters that evolve from initial values at very high energies (short distance), to fixed stable values, usually predictable, at low energies (large distance). This usually involves the use of the renormalization group, which specifically details the way parameters in a physical system (a quantum field theory) depend on the energy scale being probed.

Conversely, if the length-scale decreases and the physical parameters approach fixed values, then we have ultraviolet fixed points. The fixed points are generally independent of the initial values of the parameters over a large range of the initial values. This is known as universality.

Statistical physics

In the statistical physics of second order phase transitions, the physical system approaches an infrared fixed point that is independent of the initial short distance dynamics that defines the material. This determines the properties of the phase transition at the critical temperature, or critical point. Observables, such as critical exponents usually depend only upon dimension of space, and are independent of the atomic or molecular constituents.

Top Quark

Standard Model

There is a remarkable infrared fixed point of the coupling constants that determine the masses of very heavy quarks.^[1]^[2] In the Standard Model, quarks and leptons have "Yukawa couplings" to the Higgs boson . These determine the mass of the particle. All of the quarks' and leptons' Yukawa couplings are small compared to the top quark's Yukawa coupling. Yukawa couplings are not constants and their properties change depending on the energy scale at which they are measured, this is known as running of the constants. The dynamics of Yukawa couplings are determined by the renormalization group equation:

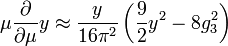$\mu \frac{\partial}{\partial\mu} y \approx \frac{y}{16\pi^2}\left(\frac{9}{2}y^2 - 8 g_3^2\right)$ ,

where 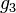$g_3$ is the color gauge coupling (which is a function of $\mu$ and associated with asymptotic freedom) and $y$ is the Yukawa coupling. This equation describes how the Yukawa coupling changes with energy scale $\mu$ .

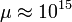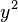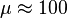The Yukawa couplings of the up, down, charm, strange and bottom quarks, are small at the extremely high energy scale of grand unification, $\mu \approx 10^{15}$ GeV. Therefore, the $y^2$ term can be neglected in the above equation. Solving, we then find that $y$ is increased slightly at the low energy scales at which the quark masses are generated by the Higgs, $\mu \approx 100$ GeV.

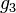On the other hand, solutions to this equation for large initial values $y$ cause the rhs to quickly approach zero . This locks $y$ to the QCD coupling $g_3$ . This is known as a (quasi-infrared) fixed point of the renormalization group equation for the Yukawa coupling. No matter what the initial starting value of the coupling is, if it is sufficiently large it will reach this fixed point value, and the corresponding quark mass is predicted.

The value of the fixed point is fairly precisely determined in the Standard Model, leading to a predicted top quark mass of 230 GeV. If there is more than one Higgs doublet, the value will be reduced by Higgs mixing angle effects. The observed top quark mass is slightly lower, about 171 GeV.

Minimal Supersymmetric Standard Model

In the minimal supersymmetric extension of the Standard Model (MSSM), there are two Higgs doublets and the renormalization group equation for the top quark Yukawa coupling is slightly modified. This leads to a fixed point where the top mass is smaller, 170–200 GeV. Some theorists believe this is supporting evidence for the MSSM.

The "quasi-infrared fixed point" was proposed in 1981 by C. T. Hill, B. Pendleton and G. G. Ross. The prevailing view at the time was that the top quark mass would lie in a range of 15 to 26 GeV. The quasi-infrared fixed point has formed the basis of top quark condensation theories of electroweak symmetry breaking in which the Higgs boson is composite at extremely short distance scales, composed of a pair of top and anti-top quarks. Many authors have explored other aspects of infrared fixed points to understand the anticipated spectrum of Higgs bosons in multi-Higgs models.

Banks-Zaks fixed point

Another example of an infrared fixed point is the Banks-Zaks fixed point in which the coupling constant of a Yang-Mills theory evolves to a fixed large value. The beta-function vanishes, and the theory possesses a symmetry known as conformal symmetry.

References

↑ Pendleton, B.; Ross, G.G. (1981). "Mass and Mixing Angle Predictions from Infrared Fixed points". Phys. Lett. B98: 291. doi:10.1016/0370-2693(81)90017-4.
↑ Hill, C.T. (1981). "Quark and Lepton masses from Renormalization group fixed points". Phys. Rev. D24: 691. doi:10.1103/PhysRevD.24.691.