Infinity (philosophy)

In philosophy, infinity can be attributed to infinite dimensions, as for instance in Kant's first antinomy. In both theology and philosophy, infinity is explored in articles such as the Ultimate, the Absolute, God, and Zeno's paradoxes. In Greek philosophy, for example in Anaximander, 'the Boundless' is the origin of all that is. He took the beginning or first principle to be an endless, unlimited primordial mass (ἄπειρον, apeiron). In Judeo-Christian theology, for example in the work of theologians such as Duns Scotus, the infinite nature of God invokes a sense of being without constraint, rather than a sense of being unlimited in quantity. In ethics infinity plays an important role designating that which cannot be defined or reduced to knowledge or power.

History

Early Indian views of infinity

The Isha Upanishad of the Yajurveda (c. 4th to 3rd century BC) states that "if you remove a part from infinity [pūrṇa] or add a part to infinity, still what remains is infinity".

The Jain mathematical text Surya Prajnapti (c. 400 BC) classifies all numbers into three sets: enumerable, innumerable, and infinite. Each of these was further subdivided into three orders:

The Jains were the first to discard the idea that all infinites were the same or equal. They recognized different types of infinities: infinite in length (one dimension), infinite in area (two dimensions), infinite in volume (three dimensions), and infinite perpetually (infinite number of dimensions).

According to Singh (1987), Joseph (2000) and Agrawal (2000), the highest enumerable number N of the Jains corresponds to the modern concept of aleph-null 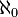\aleph_0 (the cardinal number of the infinite set of integers 1, 2, ...), the smallest cardinal transfinite number. The Jains also defined a whole system of infinite cardinal numbers, of which the highest enumerable number N is the smallest.

In the Jaina work on the theory of sets, two basic types of infinite numbers are distinguished. On both physical and ontological grounds, a distinction was made between asaṃkhyāta ("countless, innumerable") and ananta ("endless, unlimited"), between rigidly bounded and loosely bounded infinities.

Early European views of infinity

In Europe the traditional view derives from Aristotle:

... It is always possible to think of a larger number: for the number of times a magnitude can be bisected is infinite. Hence the infinite is potential, never actual; the number of parts that can be taken always surpasses any assigned number.

— Physics 207b8

This is often called potential infinity; however there are two ideas mixed up with this. One is that it is always possible to find a number of things that surpasses any given number, even if there are not actually such things. The other is that we may quantify over infinite sets without restriction. For example, \forall n \in \mathbb{Z} (\exists m \in \mathbb{Z} [m > n \wedge P(m)] ), which reads, "for any integer n, there exists an integer m > n such that P(m)". The second view is found in a clearer form by medieval writers such as William of Ockham:

Sed omne continuum est actualiter existens. Igitur quaelibet pars sua est vere existens in rerum natura. Sed partes continui sunt infinitae quia non tot quin plures, igitur partes infinitae sunt actualiter existentes.

But every continuum is actually existent. Therefore any of its parts is really existent in nature. But the parts of the continuum are infinite because there are not so many that there are not more, and therefore the infinite parts are actually existent.

The parts are actually there, in some sense. However, on this view, no infinite magnitude can have a number, for whatever number we can imagine, there is always a larger one: "There are not so many (in number) that there are no more." Aquinas also argued against the idea that infinity could be in any sense complete, or a totality.

Views from the Renaissance to modern times

Galileo

Galileo was the first to notice that we can place an infinite set into one-to-one correspondence with one of its proper subsets (any part of the set, that is not the whole). For example, we can match up the set of square numbers {1, 4, 9, 16, ...} with the natural numbers {1, 2, 3, 4, ...} as follows:

1 → 1
2 → 4
3 → 9
4 → 16
…

It appeared, by this reasoning, as though a set which is naturally smaller than the set of which it is a part (since it does not contain all the members of that set) is in some sense the same "size". Galileo thought this was one of the difficulties which arise when we try, "with our finite minds," to comprehend the infinite.

So far as I see we can only infer that the totality of all numbers is infinite, that the number of squares is infinite, and that the number of their roots is infinite; neither is the number of squares less than the totality of all numbers, nor the latter greater than the former; and finally the attributes "equal," "greater," and "less," are not applicable to infinite, but only to finite, quantities.

— On two New Sciences, 1638

The idea that size can be measured by one-to-one correspondence is today known as Hume's principle, although Hume, like Galileo, believed the principle could not be applied to infinite sets. (Mathematicians from the time of Georg Cantor do apply the principle to infinite sets, and do have a notion of some infinite quantities being greater than others.)

John Locke

Locke, in common with most of the empiricist philosophers, also believed that we can have no proper idea of the infinite. They believed all our ideas were derived from sense data or "impressions," and since all sensory impressions are inherently finite, so too are our thoughts and ideas. Our idea of infinity is merely negative or privative.

Whatever positive ideas we have in our minds of any space, duration, or number, let them be never so great, they are still finite; but when we suppose an inexhaustible remainder, from which we remove all bounds, and wherein we allow the mind an endless progression of thought, without ever completing the idea, there we have our idea of infinity... yet when we would frame in our minds the idea of an infinite space or duration, that idea is very obscure and confused, because it is made up of two parts very different, if not inconsistent. For let a man frame in his mind an idea of any space or number, as great as he will, it is plain the mind rests and terminates in that idea; which is contrary to the idea of infinity, which consists in a supposed endless progression.

— Essay, II. xvii. 7., author's emphasis

He considered that in considerations on the subject of eternity, which he classified as an infinity, humans are likely to make mistakes.[1]

Thomas Hobbes

Famously, the ultra-empiricist Hobbes tried to defend the idea of a potential infinity in light of the discovery, by Evangelista Torricelli, of a figure (Gabriel's Horn) whose surface area is infinite, but whose volume is finite. Not reported, this motivation of Hobbes came too late as curves having infinite length yet bounding finite areas were known much before. Such seeming paradoxes are resolved by taking any finite figure and stretching its content infinitely in one direction; the magnitude of its content is unchanged as its divisions drop off geometrically but the magnitude of its bounds increases to infinity by necessity. Potentiality lies in the definitions of this operation, as well-defined and interconsistent mathematical axioms. A potential infinity is allowed by letting an infinitely-large quantity be cancelled out by an infinitely-small quantity.

Modern philosophical views

Modern discussion of the infinite is now regarded as part of set theory and mathematics. This discussion is generally avoided by philosophers. An exception was Wittgenstein, who made an impassioned attack upon axiomatic set theory, and upon the idea of the actual infinite, during his "middle period".[2]

Does the relation m = 2n correlate the class of all numbers with one of its subclasses? No. It correlates any arbitrary number with another, and in that way we arrive at infinitely many pairs of classes, of which one is correlated with the other, but which are never related as class and subclass. Neither is this infinite process itself in some sense or other such a pair of classes... In the superstition that m = 2n correlates a class with its subclass, we merely have yet another case of ambiguous grammar.

— Philosophical Remarks § 141, cf Philosophical Grammar p. 465

Unlike the traditional empiricists, he thought that the infinite was in some way given to sense experience.

... I can see in space the possibility of any finite experience... we recognise [the] essential infinity of space in its smallest part." "[Time] is infinite in the same sense as the three-dimensional space of sight and movement is infinite, even if in fact I can only see as far as the walls of my room.
... what is infinite about endlessness is only the endlessness itself.

Ethics

The philosopher Emmanuel Levinas uses infinity to designate that which cannot be defined or reduced to knowledge or power. In Levinas' magnum opus Totality and Infinity he says :

...infinity is produced in the relationship of the same with the other, and how the particular and the personal, which are unsurpassable, as it were magnetize the very field in which the production of infinity is enacted...

The idea of infinity is not an incidental notion forged by a subjectivity to reflect the case of an entity encountering on the outside nothing that limits it, overflowing every limit, and thereby infinite. The production of the infinite entity is inseparable from the idea of infinity, for it is precisely in the disproportion between the idea of infinity and the infinity of which it is the idea that this exceeding of limits is produced. The idea of infinity is the mode of being, the infinition, of infinity... All knowing qua intentionality already presupposes the idea of infinity, which is preeminently non-adequation.

— p. 26-27

Levinas also wrote a work entitled Philosophy and the Idea of Infinity, which was published during 1957.[3]

Three types of infinities

Besides the mathematical infinity and the physical infinity, there could also be a philosophical infinity. There are scientists who hold that all three really exist and there are scientists who hold that none of the three exists. And in between there are the various possibilities. Rudy Rucker, in his book Infinity and the Mind—the Science and Philosophy of the Infinite (1982), has worked out a model list of representatives of each of the eight possible standpoints. The footnote on p. 335 of his book suggests the consideration of the following names: Abraham Robinson, Plato, Thomas Aquinas, L.E.J. Brouwer, David Hilbert, Bertrand Russell, Kurt Gödel and Georg Cantor.

Structure of infinity, examples from metaphysics

Notes and references

  1. ↑ Philosophical beauties selected from the works of John Locke - p.237 T.Hurst 1802 [Retrieved 2015-3-28](ed. Locke writes: And hence it is, that in disputes and reasonings concerning eternity, or any other infinite, we are apt to blunder, and involve ourselves in manifest absurdities...)
  2. ↑ See also "Logic of antinomies". Retrieved July 9, 2010.
  3. ↑ E. Levinas - Collected Philosophical Papers (p.47) (Translated by A. Lingis) Springer Science & Business Media, 31 Mar 1987 ISBN 9024733952 [Retrieved 2015-05-01]

Other references