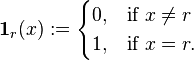Index set

In mathematics, an index set is a set whose members label (or index) members of another set.^[1]^[2] For instance, if the elements of a set A may be indexed or labeled by means of a set J, then J is an index set. The indexing consists of a surjective function from J onto A and the indexed collection is typically called an (indexed) family, often written as (A_j)_j∈J.

Examples

An enumeration of a set $S$ gives an index set 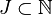$J \sub \mathbb{N}$ , where $f : J \to S$ is the particular enumeration of $S$ .

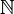Any countably infinite set can be indexed by $\mathbb{N}$ .

For 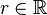$r \in \mathbb{R}$ , the indicator function on $r$ is the function $\mathbf{1}_r\colon \mathbb{R} \rarr \{0,1\}$ given by

\mathbf{1}_r (x) := \begin{cases} 0, & \mbox{if } x \ne r \\ 1, & \mbox{if } x = r. \end{cases}

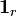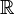The set of all the $\mathbf{1}_r$ functions is an uncountable set indexed by $\mathbb{R}$ .

Other uses

In computational complexity theory and cryptography, an index set is a set for which there exists an algorithm I that can sample the set efficiently; i.e., on input 1ⁿ, I can efficiently select a poly(n)-bit long element from the set.^[3]

References

↑ Weisstein, Eric. "Index Set". Wolfram MathWorld. Wolfram Research. Retrieved 30 December 2013.
↑ Munkres, James R. Topology. Vol. 2. Upper Saddle River: Prentice Hall, 2000.
↑ Goldreich, Oded (2001). Foundations of Cryptography: Volume 1, Basic Tools. Cambridge University Press. ISBN 0-521-79172-3.

Index set

Examples

Other uses

See also

References