Indeterminacy in concurrent computation
Indeterminacy in concurrent computation is concerned with the effects of indeterminacy in concurrent computation.
Computation is an area in which indeterminacy is becoming increasingly important because of the massive increase in concurrency due to networking and the advent of many-core computer architectures. These computer systems make use of arbiters which give rise to indeterminacy.
A limitation of logic programming
Patrick Hayes [1973] argued that the "usual sharp distinction that is made between the processes of computation and deduction, is misleading". Robert Kowalski developed the thesis that computation could be subsumed by deduction and quoted with approval "Computation is controlled deduction." which he attributed to Hayes in his 1988 paper on the early history of Prolog. Contrary to Kowalski and Hayes, Carl Hewitt claimed that logical deduction was incapable of carrying out concurrent computation in open systems.
Hewitt [1985] and Agha [1991], and other published work argued that mathematical models of concurrency did not determine particular concurrent computations as follows: The Actor model makes use of arbitration (often in the form of notional Arbiters) for determining which message is next in the arrival ordering of an Actor that is sent multiple messages concurrently. This introduces indeterminacy in the arrival order. Since the arrival orderings are indeterminate, they cannot be deduced from prior information by mathematical logic alone. Therefore mathematical logic can not implement concurrent computation in open systems.
The authors note that although mathematical logic cannot, in their view, implement general concurrency it can implement some special cases of concurrent computation, e.g., sequential computation and some kinds of parallel computation including the lambda calculus.
Arrival order indeterminacy
According to Hewitt, in concrete terms for Actor systems, typically we cannot observe the details by which the arrival order of messages for an Actor is determined. Attempting to do so affects the results and can even push the indeterminacy elsewhere. e.g., see metastability in electronics and arbiters. Instead of observing the internals of arbitration processes of Actor computations, we await outcomes. Indeterminacy in arbiters produces indeterminacy in Actors. The reason that we await outcomes is that we have no alternative because of indeterminacy.
It is important to be clear about the basis for the published claim about the limitation of mathematical logic. It was not just that Actors could not in general be implemented in mathematical logic. The published claim was that because of the indeterminacy of the physical basis of the Actor model, that no kind of deductive mathematical logic could escape the limitation. This became important later when researchers attempted to extend Prolog (which had some basis in logic programming) to concurrent computation using message passing. (See the section below).
What does the mathematical theory of Actors have to say about this? A closed system is defined to be one which does not communicate with the outside. Actor model theory provides the means to characterize all the possible computations of a closed Actor system using the Representation Theorem [Hewitt 2007] as follows:
- The mathematical denotation denoted by a closed system S is found by constructing increasingly better approximations from an initial behavior called ⊥S using a behavior approximating function progressionS to construct a denotation (meaning ) for S as follows :
- DenoteS ≡
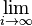 progressionSi(⊥S)
progressionSi(⊥S)
- DenoteS ≡
In this way, the behavior of S can be mathematically characterized in terms of all its possible behaviors (including those involving unbounded nondeterminism).
So mathematical logic can characterize (as opposed to implement) all the possible computations of a closed Actor system.
A limitation of logic due to lack of information
An open Actor system S is one in which the addresses of outside Actors can be passed into S in the middle of computations so that S can communicate with these outside Actors. These outside Actors can then in turn communicate with Actors internal to S using addresses supplied to them by S. Due to limitation of the inability to deduce arrival orderings, knowledge of what messages are sent from outside would not enable the response of S to be deduced. When other models of concurrent systems ( e.g., process calculi) are used to implement open systems, these systems also can have behavior that depends on arrival time orderings and so cannot be implemented by logical deduction.
Prolog-like concurrent systems were claimed to be based on mathematical logic
Keith Clark, Hervé Gallaire, Steve Gregory, Vijay Saraswat, Udi Shapiro, Kazunori Ueda, etc. developed a family of Prolog-like concurrent message passing systems using unification of shared variables and data structure streams for messages. Claims were made that these systems were based on mathematical logic. This kind of system was used as the basis of the Japanese Fifth Generation Project (ICOT).
Carl Hewitt and Gul Agha [1991] argued that these Prolog-like concurrent systems were neither deductive nor logical: like the Actor model, the Prolog-like concurrent systems were based on message passing and consequently were subject to the same indeterminacy.
Logical operations and system efficiency
Hewitt maintained that a basic lesson can be learned from Prolog and the Prolog-like concurrent systems: a universal model of concurrent computation is limited by having any mandatory overhead in the basic communication mechanisms. This is an argument against including pattern-directed invocation using unification and extraction of messages from data structure streams as fundamental primitives. But compare Shapiro's survey of Prolog-like concurrent programming languages for arguments for inclusion.
Indeterminacy in other models of computation
Arbitration is the basis of the indeterminacy in the Actor model of concurrent computation (see Actor model early history and Actor model theory). It may also play a role in other models of concurrent systems such as process calculi.
See also
- Quantum computer
- Randomized algorithm
- Nondeterministic Turing machine
References
- Carl Hewitt What is computation? Actor Model versus Turing's Model in A Computable Universe: Understanding Computation & Exploring Nature as Computation. Dedicated to the memory of Alan M. Turing on the 100th anniversary of his birth. Edited by Hector Zenil. World Scientific Publishing Company. 2012
- Carl Hewitt. PLANNER: A Language for Proving Theorems in Robots IJCAI 1969.
- Carl Hewitt. Procedural Embedding of Knowledge In Planner IJCAI 1971.
- Carl Hewitt, Peter Bishop and Richard Steiger. A Universal Modular Actor Formalism for Artificial Intelligence IJCAI 1973.
- Robert Kowalski Predicate Logic as Programming Language Memo 70, Department of Artificial Intelligence, Edinburgh University. 1973.
- Pat Hayes. Computation and Deduction Mathematical Foundations of Computer Science: Proceedings of Symposium and Summer School, Štrbské Pleso, High Tatras, Czechoslovakia, September 3–8, 1973.
- Carl Hewitt and Henry Baker Laws for Communicating Parallel Processes IFIP-77, August 1977.
- Carl Hewitt. Viewing Control Structures as Patterns of Passing Messages Journal of Artificial Intelligence. June 1977.
- Henry Baker. Actor Systems for Real-Time Computation MIT EECS Doctoral Dissertation. January 1978.
- Bill Kornfeld and Carl Hewitt. The Scientific Community Metaphor IEEE Transactions on Systems, Man and Cybernetics. January 1981.
- Will Clinger. Foundations of Actor Semantics MIT Mathematics Doctoral Dissertation. June 1981.
- Carl Hewitt. The Challenge of Open Systems Byte Magazine. April 1985. Reprinted in The foundation of artificial intelligence---a sourcebook Cambridge University Press. 1990.
- Gul Agha. Actors: A Model of Concurrent Computation in Distributed Systems Doctoral Dissertation. MIT Press. 1986.
- Robert Kowalski. The limitation of logic Proceedings of the 1986 ACM 14th Annual Conference on Computer science.
- Ehud Shapiro (Editor). Concurrent Prolog MIT Press. 1987.
- Robert Kowalski. The Early Years of Logic Programming Communications of the ACM. January 1988.
- Ehud Shapiro. The family of concurrent logic programming languages ACM Computing Surveys. September 1989.
- Carl Hewitt and Gul Agha. Guarded Horn clause languages: are they deductive and Logical? International Conference on Fifth Generation Computer Systems, Ohmsha 1988. Tokyo. Also in Artificial Intelligence at MIT, Vol. 2. MIT Press 1991.
- Carl Hewitt. *Carl Hewitt. The repeated demise of logic programming and why it will be reincarnated What Went Wrong and Why: Lessons from AI Research and Applications. Technical Report SS-06-08. AAAI Press. March 2006.
External links
- Hewitt, Meijer and Szyperski: The Actor Model (everything you wanted to know, but were afraid to ask) Microsoft Channel 9. April 9, 2012.