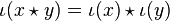Inclusion map

A is a subset of B, and B is a superset of A.

In mathematics, if $A$ is a subset of $B$ , then the inclusion map (also inclusion function, insertion, or canonical injection) ^[1] is the function $\iota$ that sends each element, $x$ of $A$ to $x$ , treated as an element of $B$ :

\iota: A\rightarrow B, \qquad \iota(x)=x.

A "hooked arrow" 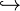$\hookrightarrow$ is sometimes used in place of the function arrow above to denote an inclusion map.

This and other analogous injective functions ^[2] from substructures are sometimes called natural injections.

Given any morphism f between objects X and Y, if there is an inclusion map into the domain 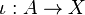$\iota : A\rightarrow X$ , then one can form the restriction fi of f. In many instances, one can also construct a canonical inclusion into the codomain R→Y known as the range of f.

Applications of inclusion maps

Inclusion maps tend to be homomorphisms of algebraic structures; thus, such inclusion maps are embeddings. More precisely, given a sub-structure closed under some operations, the inclusion map will be an embedding for tautological reasons. For example, for a binary operation 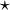$\star$ , to require that

\iota(x\star y)=\iota(x)\star \iota(y)

is simply to say that 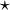$\star$ is consistently computed in the sub-structure and the large structure. The case of a unary operation is similar; but one should also look at nullary operations, which pick out a constant element. Here the point is that closure means such constants must already be given in the substructure.

Inclusion maps are seen in algebraic topology where if A is a strong deformation retract of X, the inclusion map yields an isomorphism between all homotopy groups (i.e. is a homotopy equivalence)

Inclusion maps in geometry come in different kinds: for example embeddings of submanifolds. Contravariant objects such as differential forms restrict to submanifolds, giving a mapping in the other direction. Another example, more sophisticated, is that of affine schemes, for which the inclusions

Spec(R/I) → Spec(R)

and

Spec(R/I²) → Spec(R)

may be different morphisms, where R is a commutative ring and I an ideal.

Notes

↑ Mac Lane, S.; Birkhoff, G. (1967), Algebra , page 5
↑ Chevalley, C. (1956), Fundamental Concepts of Algebra , page 1

References

Chevalley, C. (1956), Fundamental Concepts of Algebra, Academic Press, New York, ISBN 0-12-172050-0 .
Mac Lane, S.; Birkhoff, G. (1967), Algebra, AMS Chelsea Publishing, Providence, Rhode Island, ISBN 0-8218-1646-2 .

Inclusion map

Applications of inclusion maps

See also

Notes

References