Identity (music)

For other uses, see Limit (music)#Identity.
Interval-4 family 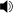 Play .
Sum-4 family 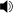 Play .

In post-tonal music theory, identity is similar to identity in universal algebra. An identity function is a permutation or transformation which transforms a pitch or pitch class set into itself. For instance, inverting an augmented triad or C4 interval cycle, 048, produces itself, 084. Performing a retrograde operation upon the pitch class set 01210 produces 01210.

In addition to being a property of a specific set, identity is, by extension, the "family" of sets or set forms which satisfy a possible identity.

George Perle provides the following example:[1]

"C-E, D-F♯, E♭-G, are different instances of the same interval [interval-4]...[an] other kind of identity...has to do with axes of symmetry. C-E belongs to a family [sum-4] of symmetrically related dyads as follows:"
D D♯ E F F♯ G G♯
D C♯ C B A♯ A G♯
2 3 4 5 6 7 8
+ 2 1 0 11 10 9 8
4 4 4 4 4 4 4

C=0, so in mod12:

1 2 3 4 5 6 7
− 9 10 11 0 1 2 3
4 4 4 4 4 4 4

Thus, in addition to being part of the interval-4 family, C-E is also a part of the sum-4 family.

See also

Sources

  1. ↑ Perle, George (1995). The Right Notes: Twenty-Three Selected Essays by George Perle on Twentieth-Century Music, p.237-238. ISBN 0-945193-37-8.