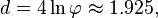Ideal triangle

Three ideal triangles in the Poincaré disk model

Two ideal triangles in the upper half-plane model

In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all lie on the circle at infinity. These vertices can be called ideal vertices. In the hyperbolic metric, any two ideal triangles are congruent. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles.

Models

In the Poincaré disk model of the hyperbolic plane, an ideal triangle is bounded by three circles which intersect the boundary circle at right angles. In the Poincaré half-plane model, an ideal triangle is modeled by an arbelos, the figure between three mutually tangent semicircles. And in the Beltrami–Klein model of the hyperbolic plane, an ideal triangle is modeled by a Euclidean triangle that is circumscribed by the boundary circle. Note that in the Beltrami-Klein model, the angles at the vertices of an ideal triangle are not zero, because the Beltrami-Klein model, unlike the Poincaré disk and half-plane models, is not conformal i.e. it does not preserve angles.

Properties

In the standard hyperbolic plane (with Gaussian curvature -1 at every point):

• The interior angles of an ideal triangle are all zero.
• Any ideal triangle has area π.^[1]
• Any ideal triangle has infinite perimeter.
• The inscribed circle to an ideal triangle meets the triangle in three points of tangency, forming an equilateral triangle with side length

where 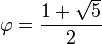is the golden ratio.^[2]

• The distance from any point in the triangle to the second-closest side of the triangle is less than or equal to d, with equality only for the three equilateral triangle vertices described above. The same inequality holds for hyperbolic triangles more generally; in a non-ideal triangle, the distance to the second-closest side is strictly less than d.

If the curvature is −K everywhere rather than −1, the areas above should be multiplied by 1/K and the lengths and distances should be multiplied by 1/√K.

Real ideal triangle group

The Poincaré disk model tiled with ideal triangles

The ideal (∞ ∞ ∞) triangle group

Another ideal tiling

The real ideal triangle group is the reflection group generated by reflections of the hyperbolic plane through the sides of an ideal triangle. Algebraically, it is isomorphic to the free product of three order-two groups (Schwarz 2001).

References

Bibliography

• Schwartz, Richard Evan (2001). "Ideal triangle groups, dented tori, and numerical analysis". Annals of Mathematics. Ser. 2 153 (3): 533–598. arXiv:math.DG/0105264. doi:10.2307/2661362. JSTOR 2661362. MR 1836282.