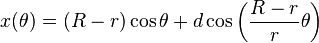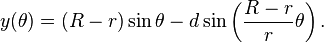Hypotrochoid

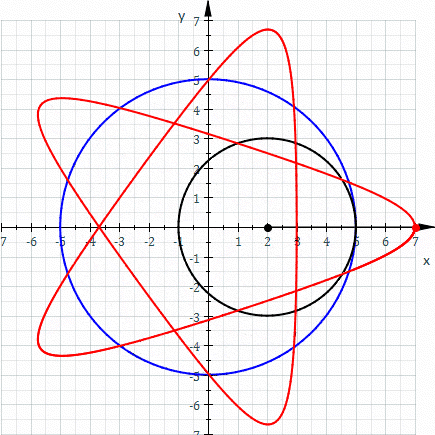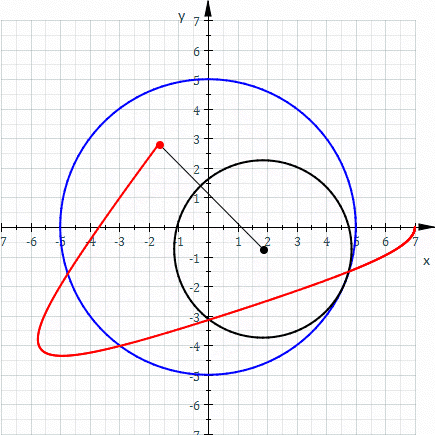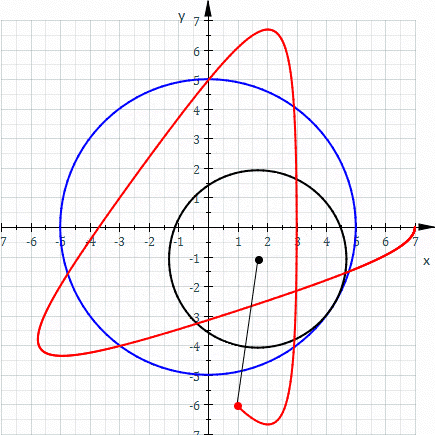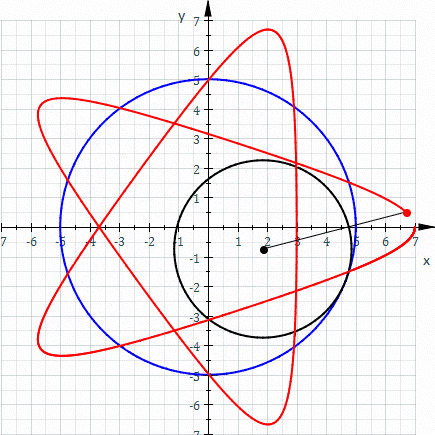
The red curve is a hypotrochoid drawn as the smaller black circle rolls around inside the larger blue circle (parameters are R = 5, r = 3, d = 5).

A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle.

The parametric equations for a hypotrochoid are:[1]

x (\theta) = (R - r)\cos\theta + d\cos\left({R - r \over r}\theta\right)
y (\theta) = (R - r)\sin\theta - d\sin\left({R - r \over r}\theta\right).

Where \theta is the angle formed by the horizontal and the center of the rolling circle (note that these are not polar equations because \theta is not the polar angle).

Special cases include the hypocycloid with d = r and the ellipse with R = 2r.

The ellipse (drawn in red) may be expressed as a special case of the hypotrochoid, with R = 2r; here R = 10, r = 5, d = 1.

The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.

See also

References

  1. ↑ J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 165–168. ISBN 0-486-60288-5.

External links