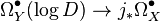Hyperhomology

In homological algebra, the hyperhomology or hypercohomology of a complex of objects of an abelian category is an extension of the usual homology of an object to complexes. It is a sort of cross between the derived functor cohomology of an object and the homology of a chain complex.

Hyperhomology is no longer used much: since about 1970 it has been largely replaced by the roughly equivalent concept of a derived functor between derived categories.

Definition

We give the definition for hypercohomology as this is more common. As usual, hypercohomology and hyperhomology are essentially the same: one converts from one to the other by dualizing, i.e. by changing the direction of all arrows, replacing injective objects with projective ones, and so on.

Suppose that A is an abelian category with enough injectives and F a left exact functor to another abelian category B. If C is a complex of objects of A bounded on the left, the hypercohomology

Hi(C)

of C (for an integer i) is calculated as follows:

  1. Take a quasi-isomorphism Φ : C → I, here I is a complex of injective elements of A.
  2. The hypercohomology Hi(C) of C is then the cohomology Hi(F(I)) of the complex F(I).

The hypercohomology of C is independent of the choice of the quasi-isomorphism, up to unique isomorphisms.

The hypercohomology can also be defined using derived categories: the hypercohomology of C is just the cohomology of F(C) considered as an element of the derived category of B.

The hypercohomology spectral sequences

There are two hypercohomology spectral sequences; one with E2 term

Hi(RjF(C))

and the other with E1 term

RjF(Ci)

and E2 term

RjF(Hi(C))

both converging to the hypercohomology

Hi+j(C),

where RjF is a right derived functor of F.

Examples

  • For a variety X over a field k, the second spectral sequence from above gives the Hodge to de Rham spectral sequence for algebraic de Rham cohomology:
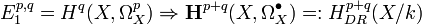    E_1^{p,q}=H^q(X,\Omega_X^p)\Rightarrow \mathbf{H}^{p+q}(X,\Omega_X^{\bullet})=:H_{DR}^{p+q}(X/k).
  • Another example comes from the holomorphic log complex on a complex manifold. Let X be a complex algebraic manifold and 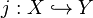j: X\hookrightarrow Y a good compactification. This means that Y is a compact algebraic manifold and 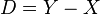D = Y-X is a divisor on Y with simple normal crossings. The natural inclusion of complexes of sheaves
    \Omega^{\bullet}_Y(\log D)\rightarrow j_*\Omega_{X}^{\bullet}

    turns out to be a quasi-isomorphism and induces an isomorphism

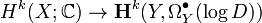    H^k(X;\mathbb{C})\rightarrow \mathbf{H}^k(Y, \Omega^{\bullet}_Y(\log D)).

See also

References