Hyperfinite set

In non-standard analysis, a branch of mathematics, a hyperfinite set or *-finite set is a type of internal set. An internal set H of internal cardinality g ∈ *N (the hypernaturals) is hyperfinite if and only if there exists an internal bijection between G = {1,2,3,...,g} and H.[1][2] Hyperfinite sets share the properties of finite sets: A hyperfinite set has minimal and maximal elements, and a hyperfinite union of a hyperfinite collection of hyperfinite sets may be derived. The sum of the elements of any hyperfinite subset of *R always exists, leading to the possibility of well-defined integration.[2]

Hyperfinite sets can be used to approximate other sets. If a hyperfinite set approximates an interval, it is called a near interval with respect to that interval. Consider a hyperfinite set K = {k_1,k_2, \dots ,k_n} with a hypernatural n. K is a near interval for [a,b] if k1 = a and kn = b, and if the difference between successive elements of K is infinitesimal. Phrased otherwise, the requirement is that for every r ∈ [a,b] there is a ki ∈ K such that ki ≈ r. 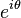This, for example, allows for an approximation to the unit circle, considered as the set e^{i\theta} for θ in the interval [0,2π].[2]

In general, subsets of hyperfinite sets are not hyperfinite, often because they do not contain the extreme elements of the parent set.[3]

Ultrapower construction

In terms of the ultrapower construction, the hyperreal line *R is defined as the collection of equivalence classes of sequences \langle u_n, n=1,2,\ldots \rangle of real numbers un. Namely, the equivalence class defines a hyperreal, denoted [u_n] in Goldblatt's notation. 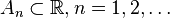Similarly, an arbitrary hyperfinite set in *R is of the form [A_n], and is defined by a sequence \langle A_n \rangle of finite sets A_n \subset \mathbb{R}, n=1,2,\ldots[4]

Notes

  1. ↑ J. E. Rubio (1994). Optimization and nonstandard analysis. Marcel Dekker. p. 110. ISBN 0-8247-9281-5.
  2. ↑ 2.0 2.1 2.2 R. Chuaqui (1991). Truth, possibility, and probability: new logical foundations of probability and statistical inference. Elsevier. pp. 182–3. ISBN 0-444-88840-3.
  3. ↑ L. Ambrosio et al. (2000). Calculus of variations and partial differential equations: topics on geometrical evolution problems and degree theory. Springer. p. 203. ISBN 3-540-64803-8.
  4. ↑ R. Goldblatt (1998). Lectures on the hyperreals. An introduction to nonstandard analysis. Springer. p. 188. ISBN 0-387-98464-X.

External links