Hypercomplex analysis
In mathematics, hypercomplex analysis is the extension of real analysis and complex analysis to the study of functions where the argument is a hypercomplex number. The first instance is functions of a quaternion variable, where the argument is a quaternion. A second instance involves functions of a motor variable where arguments are split-complex numbers.
In mathematical physics there are hypercomplex systems called Clifford algebras. The study of functions with arguments from a Clifford algebra is called Clifford analysis.
A matrix may be considered a hypercomplex number. For example, study of functions of 2 × 2 real matrices shows that the topology of the space of hypercomplex numbers determines the function theory. Functions such as square root of a matrix, matrix exponential, and logarithm of a matrix are basic examples of hypercomplex analysis.
The function theory of diagonalizable matrices is particularly transparent since they have eigendecompositions. Suppose 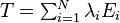 where the Ei are projections. Then for any polynomial
where the Ei are projections. Then for any polynomial 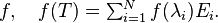
Modern terminology is algebra for "system of hypercomplex numbers", and the algebras used in applications are often Banach algebras since Cauchy sequences can be taken to be convergent. Then the function theory is enriched by sequences and series. In this context the extension of holomorphic functions of a complex variable is developed as the holomorphic functional calculus. Hypercomplex analysis on Banach algebras is called functional analysis.
References
- Daniel Alpay (editor) (2006) Wavelets, Multiscale systems and Hypercomplex Analysis, Springer, ISBN 9783764375881 .
- Enrique Ramirez de Arellanon (1998) Operator theory for complex and hypercomplex analysis, American Mathematical Society (Conference proceedings from a meeting in Mexico City in December 1994).
- Geoffrey Fox (1949) Elementary Function Theory of a Hypercomplex Variable and the Theory of Conformal Mapping in the Hyperbolic Plane, M.A. thesis, University of British Columbia.
- Sorin D. Gal (2004) Introduction to the Geometric Function theory of Hypercomplex variables, Nova Science Publishers, ISBN 1-59033-398-5.
- R. Lavika & A.G. O’ Farrell & I. Short(2007) "Reversible maps in the group of quaternionic Möbius transformations", Mathematical Proceedings of the Cambridge Philosophical Society 143:57–69.
- Birkhauser Mathematics (2011) Hypercomplex Analysis and Applications, series with editors Irene Sabadini and Franciscus Sommen.
- Irene Sabadini & Michael V. Shapiro & F. Sommen (editors) (2009) Hypercomplex Analysis, Birkhauser ISBN 978-3-7643-9892-7.
- Springer (2012) Advances in Hypercomplex Analysis, eds Sabadini, Sommen, Struppa.
External links
- Chapman University , includes Daniele Struppa, Chancellor of Chapman University, Chapman faculty, and several "external faculty".
- Roman Lavika (2011) Hypercomplex Analysis: Selected Topics (Habilitation Thesis) Charles University in Prague.