Hyperbolic secant distribution
|
Probability density function
| |
|
Cumulative distribution function
| |
| Parameters | none |
|---|---|
| Support |
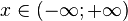 |
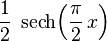 | |
| CDF |
![\frac{2}{\pi} \arctan\!\left[\exp\!\left(\frac{\pi}{2}\,x\right)\right]\!](../I/m/b52d9c3605d3f67e321f06edcb099f95.png) |
| Mean |
 |
| Median |
 |
| Mode |
 |
| Variance |
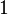 |
| Skewness |
 |
| Ex. kurtosis |
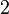 |
| Entropy |
4/π K 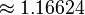 |
| MGF |
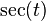 for for  |
| CF |
 for for  |
In probability theory and statistics, the hyperbolic secant distribution is a continuous probability distribution whose probability density function and characteristic function are proportional to the hyperbolic secant function. The hyperbolic secant function is equivalent to the inverse hyperbolic cosine, and thus this distribution is also called the inverse-cosh distribution.
Explanation
A random variable follows a hyperbolic secant distribution if its probability density function (pdf) can be related to the following standard form of density function by a location and shift transformation:
where "sech" denotes the hyperbolic secant function. The cumulative distribution function (cdf) of the standard distribution is
where "arctan" is the inverse (circular) tangent function. The inverse cdf (or quantile function) is
where "arsinh" is the inverse hyperbolic sine function and "cot" is the (circular) cotangent function.
The hyperbolic secant distribution shares many properties with the standard normal distribution: it is symmetric with unit variance and zero mean, median and mode, and its pdf is proportional to its characteristic function. However, the hyperbolic secant distribution is leptokurtic; that is, it has a more acute peak near its mean, and heavier tails, compared with the standard normal distribution.
Johnson et al. (1995, p147) place this distribution in the context of a class of generalised forms of the logistic distribution, but use a different parameterisation of the standard distribution compared to that here. Ding (2014) shows three occurrences of the Hyperbolic secant distribution in statistical modeling and inference.
References
- Baten, W. D. (1934). "The probability law for the sum of n independent variables, each subject to the law
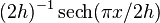 ". Bulletin of the American Mathematical Society 40 (4): 284–290. doi:10.1090/S0002-9904-1934-05852-X.
". Bulletin of the American Mathematical Society 40 (4): 284–290. doi:10.1090/S0002-9904-1934-05852-X. - J. Talacko, 1956, "Perks' distributions and their role in the theory of Wiener's stochastic variables", Trabajos de Estadistica 7:159–174.
- Luc Devroye, 1986, Non-Uniform Random Variate Generation, Springer-Verlag, New York. Section IX.7.2.
- G.K. Smyth (1994). "A note on modelling cross correlations: Hyperbolic secant regression". Biometrika 81 (2): 396–402. doi:10.1093/biomet/81.2.396.
- Norman L. Johnson, Samuel Kotz and N. Balakrishnan, 1995, Continuous Univariate Distributions, volume 2, ISBN 0-471-58494-0.
- Ding, P. 2014, "Three Occurrences of the Hyperbolic-Secant Distribution", The American Statistician, 68, 32-35.


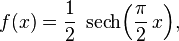
![F(x) = \frac12 + \frac{1}{\pi} \arctan\!\left[\operatorname{sinh}\!\left(\frac{\pi}{2}\,x\right)\right]
\! ,](../I/m/10176d025f520cec35ac60b3b8aed1a9.png)
![= \frac{2}{\pi} \arctan\!\left[\exp\left(\frac{\pi}{2}\,x\right)\right] \! .](../I/m/f7a173c64bc0bd31974c80a98196da66.png)
![F^{-1}(p) = -\frac{2}{\pi}\, \operatorname{arsinh}\!\left[\cot(\pi\,p)\right] \! ,](../I/m/a900ccb0380e562c8fc44b03f99a91a6.png)
![= \frac{2}{\pi}\, \ln\!\left[\tan\left(\frac{\pi}{2}\,p\right)\right] \! .](../I/m/5e47b5fd50432f7090fe1e0f97b355a7.png)