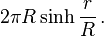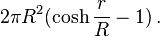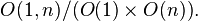Hyperbolic geometry

In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced.
The parallel postulate in Euclidean geometry is equivalent to the statement (Playfair's axiom) that, in two-dimensional space, for any given line R and point P not on R, there is exactly one line through P that does not intersect R; i.e., that is parallel to R.
In hyperbolic geometry there are at least two distinct lines through P which do not intersect R, so the parallel postulate is false.
Hyperbolic plane geometry is the geometry of saddle surfaces with a constant negative Gaussian curvature (for example the pseudosphere).
A modern use of hyperbolic geometry is in the theory of special relativity, particularly Minkowski spacetime and in gyrovector space.
History
Since the publication of Euclid's Elements circa 300 BCE, many geometers made attempts to prove the parallel postulate. A number of them made their attempts to prove the parallel postulate by assuming its negation and trying to derive a contradiction foremost among these were Proclus, Ibn al-Haytham (Alhacen), Omar Khayyám,[1] Nasīr al-Dīn al-Tūsī, Witelo, Gersonides, Alfonso, and later Giovanni Gerolamo Saccheri, John Wallis, Johann Heinrich Lambert, and Legendre.[2] Their attempts were doomed to failure (as we now know, the parallel postulate is not provable from the other postulates), but their efforts gave birth to hyperbolic geometry.
The theorems of Alhacen, Khayyam and al-Tūsī on quadrilaterals, including the Ibn al-Haytham–Lambert quadrilateral and Khayyam–Saccheri quadrilateral, were the first theorems on hyperbolic geometry. Their works on hyperbolic geometry had a considerable influence on its development among later European geometers, including Witelo, Gersonides, Alfonso, John Wallis and Saccheri.[3]
In the 18th century, Johann Heinrich Lambert introduced the hyperbolic functions[4] and computed the area of a hyperbolic triangle.[5]
In the 19th century, hyperbolic geometry was extensively explored by János Bolyai and Nikolai Ivanovich Lobachevsky, after whom it sometimes is named. Lobachevsky published in 1830, while Bolyai independently discovered it and published in 1832. Carl Friedrich Gauss also studied hyperbolic geometry, describing in an 1824 letter to Taurinus that he had constructed it, but Gauss did not publish his work. Other than their predecessors, who just wanted to eliminate the parallel postulate from the axioms of euclidean geometry Bolyai [6] and Lobachevsky realized they had discovered a new geometry.
In 1868, Eugenio Beltrami provided models of hyperbolic geometry, and used this to prove that hyperbolic geometry was consistent if and only if Euclidean geometry was.
The term "hyperbolic geometry" was introduced by Felix Klein in 1871.[7] Klein followed an initiative of Arthur Cayley to use the transformations of projective geometry to produce isometries. The idea used a conic section or quadric to define a region, and used cross ratio to define a metric . The projective transformations that leave the conic section or quadric stable are the isometries. "Klein showed that if the Cayley absolute is a real curve then the part of the projective plane in its interior is isometric to the hyperbolic plane..."[8]
For more history, see article on non-Euclidean geometry, and the references Coxeter [9] and Milnor.[10]
Philosophical consequences
The discovery of hyperbolic geometry had important philosophical consequences. Before its discovery many philosophers (for example Hobbes and Spinoza) viewed philosophical rigour in terms of the "geometrical method", referring to the method of reasoning used in Euclid's Elements.
Kant in the Critique of Pure Reason came to the conclusion that space (in Euclidean geometry) and time are not discovered by humans as objective features of the world, but are part of an unavoidable systematic framework for organizing our experiences.[11]
It is said that Gauss did not publish anything about hyperbolic geometry out of fear of the "uproar of the Boeotians " which would ruin his status.[12]
The "uproar of the Boeotians " came and went, and gave an impetus to great improvements of mathematical rigour, analytical philosophy and logic, but finally hyperbolic geometry was proved consistent and therefore another real geometry. However, this led to the question: "Is hyperbolic or Euclidean geometry the real geometry of space and if it is hyperbolic what is its curvature?" Henri Poincare, with his sphere-world thought experiment, came to the conclusion that everyday experience does not necessarily rule out other geometries. Indeed, general relativity posits that the geometry of space is in fact not Euclidean.
Properties
Hyperbolic geometry has many properties that differ from Euclidean geometry.
As mentioned above there are at least two distinct lines through P which do not intersect R. This means that there are through R an infinite number of non-intersecting lines.
These non-intersecting lines are divided into two classes: Two of them (one on each side of B) are limiting parallel they get asymptotically closer and closer to R. The other lines are called ultraparallel and will at some point diverge away from R.
The limiting parallels make an angle θ with PB, this angle depends only on the Gaussian curvature of the plane and the distance PB and is called the angle of parallelism.
For ultraparallel lines the ultraparallel theorem states that there is a unique line in the hyperbolic plane that is perpendicular to each pair of ultraparallel lines.
In hyperbolic geometry, there is no straight line whose points have the same orthogonal distance from a given straight line. (in hyperbolic geometry rectangles do not exist) Instead these points are all on a curve called a hypercycle.
Another special curve is the horocycle, a curve whose normal radii are limiting parallel and all converge asymptotically to the same ideal point.
In hyperbolic geometry, 3 distinct points lie on either a line, a hypercycle, a horocycle, or a circle.
Circles and disks
In hyperbolic geometry, the circumference of a circle of radius r is greater than 2πr. Let 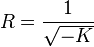 , where
, where  is the Gaussian curvature of the plane. The circumference of a circle of radius r is equal to
is the Gaussian curvature of the plane. The circumference of a circle of radius r is equal to
The area of the enclosed disk is
Triangles
Unlike Euclidean triangles whose angles always add up to 180°; the sum of the angles of a hyperbolic triangle is always strictly less than 180° or π radians. The difference is sometimes referred to as the defect.
The area of a hyperbolic triangle is given by its defect in radians multiplied by 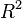 where
where 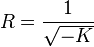 and
and  is the Gaussian curvature of the plane.
is the Gaussian curvature of the plane.
As a consequence all hyperbolic triangles have an area which is less than 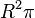 .
The area of a hyperbolic ideal triangle in which all three angles are 0° is equal to this maximum.
.
The area of a hyperbolic ideal triangle in which all three angles are 0° is equal to this maximum.
As in Euclidean geometry each hyperbolic triangle has an inscribed circle.
But if its vertices lie on an horocycle or hypercycle, the triangle has no circumscribed circle.
As in spherical geometry the only similar triangles are congruent triangles.
Standardized Gaussian curvature
While in principle hyperbolic geometry is valid on any surface with a constant negative Gaussian curvature it is usual to model hyperbolic geometry with a curvature  of
of 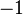 .
.
This results that: formula's become simpler, examples:
The area of a triangle is equal to its angle defect in radians,
The length of an arc of an horocycle such that the tangent at one extremity is limiting parallel to the radius through the other extremity is 1 [13]
The ratio of the arclengths between two radii of two horocycles where the horocycles are a distance 1 apart is e : 1.[14]
Models of the hyperbolic plane
By Hilbert's theorem it is not possible to create a complete hyperbolic plane (a complete regular surface of constant negative Gaussian curvature) in Euclidean space.
There are different pseudospherical surfaces that have for a large area a constant negative Gaussian curvature, the pseudosphere being the best well known of them.
But it is easier to do hyperbolic geometry on other models.

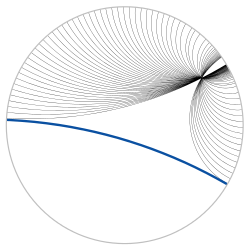
There are four models commonly used for hyperbolic geometry: the Klein model, the Poincaré disc model, the Poincaré half-plane model, and the Lorentz model, or hyperboloid model. These models define a real hyperbolic space which satisfies the axioms of a hyperbolic geometry. Despite their names, the first three mentioned above were introduced as models of hyperbolic space by Beltrami, not by Poincaré or Klein. All these models generalize to more dimensions.
The Beltrami–Klein model
The Beltrami–Klein model, also known as the projective disc model and Klein model, is named after Eugenio Beltrami and Felix Klein.
This model uses the interior of the unit circle for the complete hyperbolic plane, and chords of this circle are the hyperbolic lines.
- This model has the advantage that lines are straight, but the disadvantage that angles are distorted (the mapping is not conformal), and also circles are not represented as circles.
- The distance in this model is half the logarithm of the cross-ratio, which was introduced by Arthur Cayley in projective geometry.
The Poincaré disc model
The Poincaré disc model, also known as the conformal disc model, also employs the interior of the unit circle, but lines are represented by arcs of circles that are orthogonal to the boundary circle, plus diameters of the boundary circle.
- This model preserves hyperbolic angles, and is thereby conformal. All isometries within these models are therefore Möbius transformations.
- Circles entirely within the disc remain circles although the Euclidean center of the circle is closer to the center of the disc than the hyperbolic center of the circle.
- Horocycles are circles within the disc which are tangent to the boundary circle, minus the point of contact.
- hypercycles are open-ended chords and circular arcs within the disc that terminate on the boundary circle at non-orthogonal angles.
The Poincaré half-plane model
The Poincaré half-plane model takes one-half of the Euclidean plane, as determined by a Euclidean line B, to be the hyperbolic plane (B itself is not included).
- Hyperbolic lines are then either half-circles orthogonal to B or rays perpendicular to B.
- Both Poincaré models preserve hyperbolic angles, and are thereby conformal. All isometries within these models are therefore Möbius transformations.
- The half-plane model is the limit of Poincaré disc models whose boundary is tangent to B at the same point while the radius of the disc model goes to infinity.
The hyperboloid model
The hyperboloid model or Lorentz model employs a 2-dimensional hyperboloid of revolution (of two sheets, but using one) embedded in 3-dimensional Minkowski space. This model is generally credited to Poincaré, but Reynolds (see reference) says that Wilhelm Killing and Karl Weierstrass used this model from 1872.[15]
- This model has direct application to special relativity, as Minkowski 3-space is a model for spacetime, suppressing one spatial dimension. One can take the hyperboloid to represent the events that various moving observers, radiating outward in a spatial plane from a single point, will reach in a fixed proper time.
- The hyperbolic distance between two points on the hyperboloid can then be identified with the relative rapidity between the two corresponding observers.
- The model generalizes directly to an additional dimension, where three-dimensional hyperbolic geometry relates to Minkowski 4-space.
Other models of the hyperbolic plane
The hemispherical model
The hemispherical model is not often used as model by itself, but it functions as a useful tool for visualising transformations between the other models.
The hemispherical model uses the upper half of the sphere:
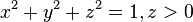
The hemisphere model is part of an Riemann sphere, and different projections give different models of the hyperbolic plane:
- Stereographic projection from
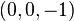 onto the plane
onto the plane  projects corresponding points on the Poincaré disk model
projects corresponding points on the Poincaré disk model
- Stereographic projection from
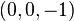 onto the surface
onto the surface 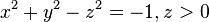 projects corresponding points on the hyperboloid model
projects corresponding points on the hyperboloid model
- stereographic projection from
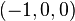 onto the plane
onto the plane 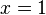 projects corresponding points on the Poincaré half-plane model
projects corresponding points on the Poincaré half-plane model
- Orthographic projection onto a plane
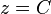 projects corresponding points on the Beltrami–Klein model.
projects corresponding points on the Beltrami–Klein model.
- Central projection from the centre of the sphere onto the plane
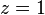 projects corresponding points on the Gans Model
projects corresponding points on the Gans Model
See further: Connection between the models (below)
The Gans Model
The Gans model or flattened hyperboloid model In 1966 David Gans proposed this model in the journal American Mathematical Monthly [16] It is an orthographic projection of the hyperboloid model onto the xy-plane. This model is not as widely used as other models but nevertheless is quite useful in the understanding of hyperbolic geometry.
- Unlike the Klein or the Poincaré models, this model utilizes the entire Euclidean plane.
- The lines in this model are interpreted as the branches of a hyperbola.[17]
Connection between the models
 Poincaré disk, hemispherical and hyperboloid models are related by stereographic projection from −1. Beltrami–Klein model is orthographic projection from hemispheric model. Poincaré half-plane model here projected from the hemisphere model by rays from left end of Poincaré disk model.
Poincaré disk, hemispherical and hyperboloid models are related by stereographic projection from −1. Beltrami–Klein model is orthographic projection from hemispheric model. Poincaré half-plane model here projected from the hemisphere model by rays from left end of Poincaré disk model.
All models essentially describe the same structure. The difference between them is that they represent different coordinate charts laid down on the same metric space, namely the hyperbolic space. The characteristic feature of the hyperbolic space itself is that it has a constant negative Gaussian curvature, which is indifferent to the coordinate chart used. The geodesics are similarly invariant: that is, geodesics map to geodesics under coordinate transformation. Hyperbolic geometry generally is introduced in terms of the geodesics and their intersections on the hyperbolic space.[18]
Once we choose a coordinate chart (one of the "models"), we can always embed it in a Euclidean space of same dimension, but the embedding is clearly not isometric (since the curvature of Euclidean space is 0). The hyperbolic space can be represented by infinitely many different charts; but the embeddings in Euclidean space due to these four specific charts show some interesting characteristics.
Since the four models describe the same metric space, each can be transformed into the other.
See, for example:
- the Beltrami–Klein model's relation to the hyperboloid model,
- the Beltrami–Klein model's relation to the Poincaré disk model,
- and the Poincaré disk model's relation to the hyperboloid model.
Visualizing hyperbolic geometry

M. C. Escher's famous prints Circle Limit III and Circle Limit IV illustrate the conformal disc model (Poincaré disk model) quite well. The white lines in III are not quite geodesics (they are hypercycles), but are quite close to them. It is also possible to see quite plainly the negative curvature of the hyperbolic plane, through its effect on the sum of angles in triangles and squares.
For example, in Circle Limit III every vertex belongs to three triangles and three squares. In the Euclidean plane, their angles would sum to 450°; i.e., a circle and a quarter. From this we see that the sum of angles of a triangle in the hyperbolic plane must be smaller than 180°. Another visible property is exponential growth. In Circle Limit III, for example, one can see that the number of fishes within a distance of n from the center rises exponentially. The fishes have equal hyperbolic area, so the area of a ball of radius n must rise exponentially in n.


There are several ways to physically realize a hyperbolic plane (or approximation thereof). A particularly well-known paper model based on the pseudosphere is due to William Thurston. The art of crochet has been used to demonstrate hyperbolic planes with the first being made by Daina Taimina,[19] whose book Crocheting Adventures with Hyperbolic Planes won the 2009 Bookseller/Diagram Prize for Oddest Title of the Year.[20] In 2000, Keith Henderson demonstrated a quick-to-make paper model dubbed the "hyperbolic soccerball". Instructions on how to make a hyperbolic quilt, designed by Helaman Ferguson,[21] has been made available by Jeff Weeks.[22]
Higher dimensions
Hyperbolic geometry in not limited to 2 dimensions, it can as all geometries be expanded to any number of dimensions.....
Homogeneous structure
Hyperbolic space of dimension n is a special case of a Riemannian symmetric space of noncompact type, as it is isomorphic to the quotient
The orthogonal group O(1, n) acts by norm-preserving transformations on Minkowski space R1,n, and it acts transitively on the two-sheet hyperboloid of norm 1 vectors. Timelike lines (i.e., those with positive-norm tangents) through the origin pass through antipodal points in the hyperboloid, so the space of such lines yields a model of hyperbolic n-space. The stabilizer of any particular line is isomorphic to the product of the orthogonal groups O(n) and O(1), where O(n) acts on the tangent space of a point in the hyperboloid, and O(1) reflects the line through the origin. Many of the elementary concepts in hyperbolic geometry can be described in linear algebraic terms: geodesic paths are described by intersections with planes through the origin, dihedral angles between hyperplanes can be described by inner products of normal vectors, and hyperbolic reflection groups can be given explicit matrix realizations.
In small dimensions, there are exceptional isomorphisms of Lie groups that yield additional ways to consider symmetries of hyperbolic spaces. For example, in dimension 2, the isomorphisms SO+(1, 2) ≅ PSL(2, R) ≅ PSU(1, 1) allow one to interpret the upper half plane model as the quotient SL(2, R)/SO(2) and the Poincaré disc model as the quotient SU(1, 1)/U(1). In both cases, the symmetry groups act by fractional linear transformations, since both groups are the orientation-preserving stabilizers in PGL(2, C) of the respective subspaces of the Riemann sphere. The Cayley transformation not only takes one model of the hyperbolic plane to the other, but realizes the isomorphism of symmetry groups as conjugation in a larger group. In dimension 3, the fractional linear action of PGL(2, C) on the Riemann sphere is identified with the action on the conformal boundary of hyperbolic 3-space induced by the isomorphism O+(1, 3) ≅ PGL(2, C). This allows one to study isometries of hyperbolic 3-space by considering spectral properties of representative complex matrices. For example, parabolic transformations are conjugate to rigid translations in the upper half-space model, and they are exactly those transformations that can be represented by unipotent upper triangular matrices.
See also
Notes
- ↑ See for instance, "Omar Khayyam 1048–1131". Retrieved 2008-01-05.
- ↑ http://www.math.columbia.edu/~pinkham/teaching/seminars/NonEuclidean.html
- ↑ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, p. 447–494 [470], Routledge, London and New York:
"Three scientists, Ibn al-Haytham, Khayyam and al-Tūsī, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the nineteenth century. In essence their propositions concerning the properties of quadrangles which they considered assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines – made by Witelo, the Polish scientists of the thirteenth century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir) – was undoubtedly prompted by Arabic sources. The proofs put forward in the fourteenth century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated both J. Wallis's and G. Saccheri's studies of the theory of parallel lines."
- ↑ Eves, Howard (2012), Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications, p. 59, ISBN 9780486132204,
We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
- ↑ Ratcliffe, John (2006), Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer, p. 99, ISBN 9780387331973,
That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
- ↑ Greenberg, Marvin Jay (2003). Euclidean and non-Euclidean geometries : development and history (3rd ed. ed.). New York: Freeman. p. 177. ISBN 0716724464.
Out of nothing I have created a strange new universe. JANOS BOLYAI
- ↑ F. Klein, Über die sogenannte Nicht-Euklidische, Geometrie, Math. Ann. 4, 573–625 (cf. Ges. Math. Abh. 1, 244–350).
- ↑ Rosenfeld, B.A. (1988) A History of Non-Euclidean Geometry, page 236, Springer-Verlag ISBN 0-387-96458-4
- ↑ Coxeter, H. S. M., (1942) Non-Euclidean geometry, University of Toronto Press, Toronto .
- ↑ Milnor, John W., (1982) Hyperbolic geometry: The first 150 years, Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24.
- ↑ Lucas, John Randolph. Space, Time and Causality. p. 149. ISBN 0-19-875057-9.
- ↑ Torretti, Roberto (1978). Philosophy of Geometry from Riemann to Poincare. Dordrecht Holland: Reidel. p. 255.
- ↑ Sommerville, D.M.Y. (2005). The elements of non-Euclidean geometry (Unabr. and unaltered republ. ed.). Mineola, N.Y.: Dover Publications. p. 58. ISBN 0-486-44222-5.
- ↑ Sommerville, D.M.Y. (2005). The elements of non-Euclidean geometry (Unabr. and unaltered republ. ed.). Mineola, N.Y.: Dover Publications. p. 58. ISBN 0-486-44222-5.
- ↑ Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid, American Mathematical Monthly 100:442–455.
- ↑ [Gans David (1966). A New Model of the Hyperbolic Plane. American Mathematical Monthly, Vol. 73, Issue 3, March 1966.
- ↑ http://www.d.umn.edu/cs/thesis/kedar_bhumkar_ms.pdf
- ↑ Arlan Ramsay, Robert D. Richtmyer, Introduction to Hyperbolic Geometry, Springer; 1 edition (December 16, 1995)
- ↑ "Hyperbolic Space". The Institute for Figuring. December 21, 2006. Retrieved January 15, 2007.
- ↑ Bloxham, Andy (March 26, 2010). "Crocheting Adventures with Hyperbolic Planes wins oddest book title award". The Telegraph.
- ↑ "Helaman Ferguson, Hyperbolic Quilt".
- ↑ "How to sew a Hyperbolic Blanket".
References
| Wikimedia Commons has media related to Hyperbolic geometry. |
- A'Campo, Norbert and Papadopoulos, Athanase, (2012) Notes on hyperbolic geometry, in: Strasbourg Master class on Geometry, pp. 1–182, IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18, Zürich: European Mathematical Society (EMS), 461 pages, SBN ISBN 978-3-03719-105-7, DOI 10.4171/105.
- Coxeter, H. S. M., (1942) Non-Euclidean geometry, University of Toronto Press, Toronto
- Fenchel, Werner (1989). Elementary geometry in hyperbolic space. De Gruyter Studies in mathematics 11. Berlin-New York: Walter de Gruyter & Co.
- Fenchel, Werner; Nielsen, Jakob; edited by Asmus L. Schmidt (2003). Discontinuous groups of isometries in the hyperbolic plane. De Gruyter Studies in mathematics 29. Berlin: Walter de Gruyter & Co.
- Lobachevsky, Nikolai I., (2010) Pangeometry, Edited and translated by Athanase Papadopoulos, Heritage of European Mathematics, Vol. 4. Zürich: European Mathematical Society (EMS). xii, 310~p, ISBN 978-3-03719-087-6/hbk
- Milnor, John W., (1982) Hyperbolic geometry: The first 150 years, Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24.
- Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid, American Mathematical Monthly 100:442–455.
- Stillwell, John (1996). Sources of hyperbolic geometry. History of Mathematics 10. Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-0529-9. MR 1402697 .
- Samuels, David., (March 2006) Knit Theory Discover Magazine, volume 27, Number 3.
- James W. Anderson, Hyperbolic Geometry, Springer 2005, ISBN 1-85233-934-9
- James W. Cannon, William J. Floyd, Richard Kenyon, and Walter R. Parry (1997) Hyperbolic Geometry, MSRI Publications, volume 31.
External links
- Java freeware for creating sketches in both the Poincaré Disk and the Upper Half-Plane Models of Hyperbolic Geometry University of New Mexico
- "The Hyperbolic Geometry Song" A short music video about the basics of Hyperbolic Geometry available at YouTube.
- Hazewinkel, Michiel, ed. (2001), "Lobachevskii geometry", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Gauss–Bolyai–Lobachevsky Space", MathWorld.
- Weisstein, Eric W., "Hyperbolic Geometry", MathWorld.
- More on hyperbolic geometry, including movies and equations for conversion between the different models University of Illinois at Urbana-Champaign
- Hyperbolic Voronoi diagrams made easy, Frank Nielsen
- Stothers, Wilson (2000). "Hyperbolic geometry". University of Glasgow., interactive instructional website.
- Universal Hyperbolic Geometry II: A pictorial overview
- Universal Hyperbolic Geometry III: First Steps in Projective Triangle Geometry
- Hyperbolic Planar Tesselations