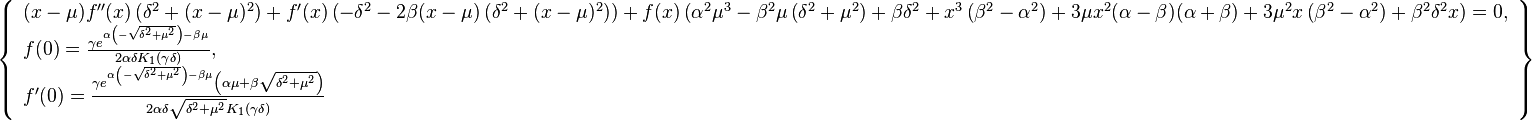Hyperbolic distribution

hyperbolic
Parameters \mu location (real)
\alpha (real)
\beta asymmetry parameter (real)
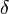\delta scale parameter (real)
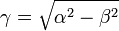\gamma = \sqrt{\alpha^2 - \beta^2}
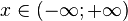Support x \in (-\infty; +\infty)\!
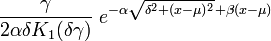PDF \frac{\gamma}{2\alpha\delta K_1(\delta \gamma)} \; e^{-\alpha\sqrt{\delta^2 + (x - \mu)^2}+ \beta (x - \mu)}

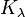K_\lambda denotes a modified Bessel function of the second kind
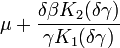Mean \mu + \frac{\delta \beta K_{2}(\delta \gamma)}{\gamma K_1(\delta\gamma)}
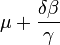Mode \mu + \frac{\delta\beta}{\gamma}
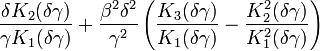Variance \frac{\delta K_{2}(\delta \gamma)}{\gamma K_1(\delta\gamma)} + \frac{\beta^2\delta^2}{\gamma^2}\left(\frac{K_{3}(\delta\gamma)}{K_{1}(\delta\gamma)} -\frac{K_{2}^2(\delta\gamma)}{K_{1}^2(\delta\gamma)} \right)
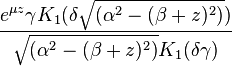MGF \frac{e^{\mu z}\gamma K_1(\delta \sqrt{ (\alpha^2 -(\beta +z)^2)})}{\sqrt{(\alpha^2 -(\beta +z)^2)}K_1 (\delta \gamma)}

The hyperbolic distribution is a continuous probability distribution characterized by the logarithm of the probability density function being a hyperbola. Thus the distribution decreases exponentially, which is more slowly than the normal distribution. It is therefore suitable to model phenomena where numerically large values are more probable than is the case for the normal distribution. Examples are returns from financial assets and turbulent wind speeds. The hyperbolic distributions form a subclass of the generalised hyperbolic distributions.

The origin of the distribution is the observation by Ralph Alger Bagnold, published in his book The Physics of Blown Sand and Desert Dunes (1941), that the logarithm of the histogram of the empirical size distribution of sand deposits tends to form a hyperbola. This observation was formalised mathematically by Ole Barndorff-Nielsen in a paper in 1977,[1] where he also introduced the generalised hyperbolic distribution, using the fact the a hyperbolic distribution is a random mixture of normal distributions.

Properties

Differential equation

The pdf of the hyperbolic distribution is a solution of the following differential equation:

\left\{\begin{array}{l} (x-\mu ) f''(x) \left(\delta^2+(x-\mu)^2\right)+f'(x) \left(-\delta ^2-2 \beta (x-\mu) \left(\delta^2+(x-\mu)^2\right)\right)+f(x) \left(\alpha ^2 \mu ^3-\beta^2 \mu \left(\delta^2+\mu^2\right)+\beta \delta^2+x^3 \left(\beta^2-\alpha^2\right)+ 3 \mu x^2 (\alpha-\beta) (\alpha+\beta)+3 \mu^2 x \left(\beta^2-\alpha^2\right)+ \beta^2 \delta^2 x\right)=0, \\ f(0)=\frac{\gamma e^{\alpha \left(-\sqrt{\delta ^2+\mu^2}\right)-\beta \mu}} {2 \alpha \delta K_1(\gamma \delta)}, \\ f'(0)=\frac{\gamma e^{\alpha \left(-\sqrt{\delta^2+\mu^2}\right)-\beta \mu} \left(\alpha \mu+\beta \sqrt{\delta^2+\mu^2}\right)}{2 \alpha \delta \sqrt{\delta^2+\mu^2} K_1(\gamma \delta)} \end{array}\right\}

References

  1. ↑ Barndorff-Nielsen, Ole (1977). "Exponentially decreasing distributions for the logarithm of particle size". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (The Royal Society) 353 (1674): 401–409. doi:10.1098/rspa.1977.0041. JSTOR 79167.