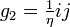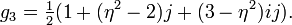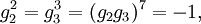Hurwitz quaternion order
The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces.[1] The Hurwitz quaternion order was studied in 1967 by Goro Shimura,[2] but first explicitly described by Noam Elkies in 1998.[3] For an alternative use of the term, see Hurwitz quaternion (both usages are current in the literature).
Definition
Let  be the maximal real subfield of
be the maximal real subfield of 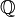
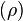 where
where  is a 7th-primitive root of unity.
The ring of integers of
is a 7th-primitive root of unity.
The ring of integers of  is
is ![\mathbb{Z}[\eta]](../I/m/bd805bc760f5976b354f339c77146139.png) , where the element
, where the element 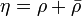 can be identified with the positive real
can be identified with the positive real 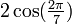 . Let
. Let  be the quaternion algebra, or symbol algebra
be the quaternion algebra, or symbol algebra
so that 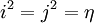 and
and 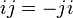 in
in  Also let
Also let 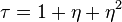 and
and 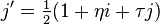 . Let
. Let
Then 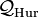 is a maximal order of
is a maximal order of  , described explicitly by Noam Elkies.[4]
, described explicitly by Noam Elkies.[4]
Module structure
The order 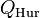 is also generated by elements
is also generated by elements
and
In fact, the order is a free ![\mathbb Z[\eta]](../I/m/e02228c1548f35d19589f07d17d70840.png) -module over
the basis
-module over
the basis 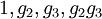 . Here the generators satisfy the relations
. Here the generators satisfy the relations
which descend to the appropriate relations in the (2,3,7) triangle group, after quotienting by the center.
Principal congruence subgroups
The principal congruence subgroup defined by an ideal ![I \subset \mathbb{Z}[\eta]](../I/m/797aee024dab07dec4b217d61677974c.png) is by definition the group
is by definition the group
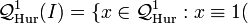 mod
mod 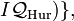
namely, the group of elements of reduced norm 1 in 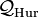 equivalent to 1 modulo the ideal
equivalent to 1 modulo the ideal 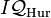 . The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
. The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
Application
The order was used by Katz, Schaps, and Vishne[5] to construct a family of Hurwitz surfaces satisfying an asymptotic lower bound for the systole: 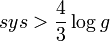 where g is the genus, improving an earlier result of Peter Buser and Peter Sarnak;[6] see systoles of surfaces.
where g is the genus, improving an earlier result of Peter Buser and Peter Sarnak;[6] see systoles of surfaces.
See also
References
- ↑ Vogeler, Roger (2003), On the geometry of Hurwitz surfaces, PhD thesis, Florida State University.
- ↑ Shimura, Goro (1967), "Construction of class fields and zeta functions of algebraic curves", Annals of Mathematics, Second Series 85: 58–159, doi:10.2307/1970526, MR 0204426.
- ↑ Elkies, Noam D. (1998), "Shimura curve computations", Algorithmic number theory (Portland, OR, 1998), Lecture Notes in Computer Science 1423, Berlin: Springer-Verlag, pp. 1–47, arXiv:math.NT/0005160, doi:10.1007/BFb0054850, MR 1726059.
- ↑ Elkies, Noam D. (1999), "The Klein quartic in number theory", The eightfold way, Math. Sci. Res. Inst. Publ. 35, Cambridge: Cambridge Univ. Press, pp. 51–101, MR 1722413.
- ↑ Katz, Mikhail G.; Schaps, Mary; Vishne, Uzi (2007), "Logarithmic growth of systole of arithmetic Riemann surfaces along congruence subgroups", Journal of Differential Geometry 76 (3): 399–422, arXiv:math.DG/0505007, MR 2331526.
- ↑ Buser, P.; Sarnak, P. (1994), "On the period matrix of a Riemann surface of large genus", Inventiones Mathematicae 117 (1): 27–56, doi:10.1007/BF01232233, MR 1269424. With an appendix by J. H. Conway and N. J. A. Sloane.
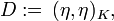
![\mathcal{Q}_{\mathrm{Hur}}=\mathbb{Z}[\eta][i,j,j'].](../I/m/8785a8b1f7542880204c79ae68ec89ef.png)