Hopf manifold

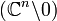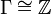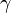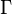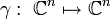In complex geometry, a Hopf manifold (Hopf 1948) is obtained as a quotient of the complex vector space (with zero deleted) ({\Bbb C}^n\backslash 0) by a free action of the group \Gamma \cong {\Bbb Z} of integers, with the generator \gamma of \Gamma acting by holomorphic contractions. Here, a holomorphic contraction is a map \gamma:\; {\Bbb C}^n \mapsto {\Bbb C}^n such that a sufficiently big iteration 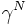\;\gamma^N puts any given compact subset 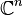{\Bbb C}^n onto an arbitrarily small neighbourhood of 0.

Two dimensional Hopf manifolds are called Hopf surfaces.

Examples

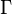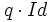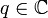In a typical situation, \Gamma is generated by a linear contraction, usually a diagonal matrix q\cdot Id, with q\in {\Bbb C} a complex number, 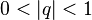0<|q|<1. Such manifold is called a classical Hopf manifold.

Properties

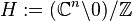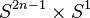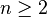A Hopf manifold H:=({\Bbb C}^n\backslash 0)/{\Bbb Z} is diffeomorphic to S^{2n-1}\times S^1. For n\geq 2, it is non-Kähler. In fact, it is not even symplectic because the second cohomology group is zero.

Hypercomplex structure

Even-dimensional Hopf manifolds admit hypercomplex structure. The Hopf surface is the only compact hypercomplex manifold of quaternionic dimension 1 which is not hyperkähler.

References