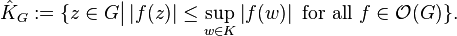Holomorphically convex hull

In mathematics, more precisely in complex analysis, the holomorphically convex hull of a given compact set in the n-dimensional complex space Cⁿ is defined as follows.

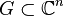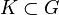Let $G \subset {\mathbb{C}}^n$ be a domain (an open and connected set), or alternatively for a more general definition, let $G$ be an $n$ dimensional complex analytic manifold. Further let ${\mathcal{O}}(G)$ stand for the set of holomorphic functions on $G.$ For a compact set $K \subset G$ , the holomorphically convex hull of $K$ is

\hat{K}_G := \{ z \in G \big| \left| f(z) \right| \leq \sup_{w \in K} \left| f(w) \right| \mbox{ for all } f \in {\mathcal{O}}(G) \} .

(One obtains a narrower concept of polynomially convex hull by requiring in the above definition that f be a polynomial.)

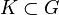The domain $G$ is called holomorphically convex if for every $K \subset G$ compact in 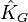$G$ , $\hat{K}_G$ is also compact in $G$ . Sometimes this is just abbreviated as holomorph-convex.

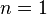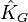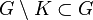When $n=1$ , any domain $G$ is holomorphically convex since then $\hat{K}_G$ is the union of $K$ with the relatively compact components of $G \setminus K \subset G$ . Also note that being holomorphically convex is the same as being a domain of holomorphy (The Cartan–Thullen theorem). These concepts are more important in the case n > 1 of several complex variables.

References

Lars Hörmander. An Introduction to Complex Analysis in Several Variables, North-Holland Publishing Company, New York, New York, 1973.
Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.

This article incorporates material from Holomorphically convex on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Holomorphically convex hull

See also

References