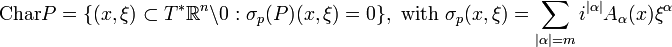Holmgren's uniqueness theorem

In the theory of partial differential equations, Holmgren's uniqueness theorem, or simply Holmgren's theorem, named after the Swedish mathematician Erik Albert Holmgren (1873–1943), is a uniqueness result for linear partial differential equations with real analytic coefficients.[1]

Simple form of Holmgren's theorem

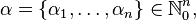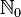We will use the multi-index notation: Let \alpha=\{\alpha_1,\dots,\alpha_n\}\in \N_0^n,, with \N_0 standing for the nonnegative integers; denote 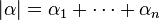|\alpha|=\alpha_1+\cdots+\alpha_n and

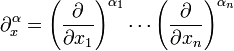\partial_x^\alpha = \left(\frac{\partial}{\partial x_1}\right)^{\alpha_1} \cdots \left(\frac{\partial}{\partial x_n}\right)^{\alpha_n}\,.

Holmgren's theorem in its simpler form could be stated as follows:

Assume that P = ∑|α| ≤m Aα(x)∂α
x is an elliptic partial differential operator with real-analytic coefficients. If Pu is real-analytic in a connected open neighborhood Ω ⊂ Rn, then u is also real-analytic.

This statement, with "analytic" replaced by "smooth", is Hermann Weyl's classical lemma on elliptic regularity:[2]

If P is an elliptic differential operator and Pu is smooth in Ω, then u is also smooth in Ω.

This statement can be proved using Sobolev spaces.

Classical form

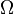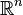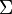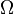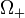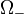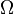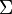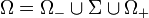Let \Omega\, be a connected open neighborhood in \R^n\,, and let \Sigma\, be an analytic hypersurface in \Omega\,, such that there are two open subsets \Omega_{+}\, and \Omega_{-}\, in \Omega\,, nonempty and connected, not intersecting \Sigma\, nor each other, such that \Omega=\Omega_{-}\cup\Sigma\cup\Omega_{+}\,.

Let 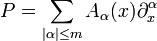P=\sum_{|\alpha|\le m}A_\alpha(x)\partial_x^\alpha\, be a differential operator with real-analytic coefficients.

Assume that the hypersurface 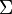\Sigma\, is noncharacteristic with respect to 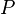P\, at every one of its points:

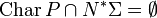\mathop{\rm Char}P\cap N^*\Sigma=\emptyset.

Above,

\mathop{\rm Char}P=\{(x,\xi)\subset T^*\R^n\backslash 0:\sigma_p(P)(x,\xi)=0\},\text{ with }\sigma_p(x,\xi)=\sum_{|\alpha|=m}i^{|\alpha|}A_\alpha(x)\xi^\alpha\,

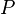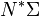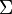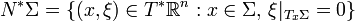the principal symbol of P\,. N^*\Sigma\, is a conormal bundle to \Sigma\,, defined as N^*\Sigma=\{(x,\xi)\in T^*\R^n:x\in\Sigma,\,\xi|_{T_x\Sigma}=0\}\,.

The classical formulation of Holmgren's theorem is as follows:

Holmgren's theorem
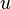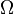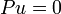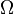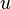Let u\, be a distribution in \Omega\, such that Pu=0\, in \Omega\,. If u\, vanishes in 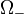\Omega_{-}\,, then it vanishes in an open neighborhood of 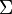\Sigma\,.[3]

Relation to the Cauchy–Kowalevski theorem

Consider the problem

\partial_t^m u=F(t,x,\partial_x^\alpha\,\partial_t^k u), \quad \alpha\in\N_0^n, \quad k\in\N_0, \quad |\alpha|+k\le m, \quad k\le m-1,

with the Cauchy data

\partial_t^k u|_{t=0}=\phi_k(x), \qquad 0\le k\le m-1,

Assume that 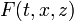F(t,x,z)\, is real-analytic with respect to all its arguments in the neighborhood of 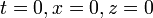t=0,x=0,z=0\, and that 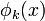\phi_k(x)\, are real-analytic in the neighborhood of x=0\,.

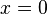Theorem (Cauchy–Kowalevski)
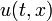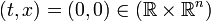There is a unique real-analytic solution u(t,x)\, in the neighborhood of (t,x)=(0,0)\in(\R\times\R^n)\,.

Note that the Cauchy–Kowalevski theorem does not exclude the existence of solutions which are not real-analytic.

On the other hand, in the case when 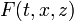F(t,x,z)\, is polynomial of order one in 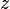z\,, so that

\partial_t^m u = F(t,x,\partial_x^\alpha\,\partial_t^k u) = \sum_{\alpha\in\N_0^n,0\le k\le m-1, |\alpha| + k\le m}A_{\alpha,k}(t,x) \, \partial_x^\alpha \, \partial_t^k u,\,

Holmgren's theorem states that the solution 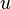u\, is real-analytic and hence, by the Cauchy–Kowalevski theorem, is unique.

See also

References

  1. ↑ Eric Holmgren, "Über Systeme von linearen partiellen Differentialgleichungen", Öfversigt af Kongl. Vetenskaps-Academien Förhandlinger, 58 (1901), 91–103.
  2. ↑ Stroock, W. (2008). "Weyl's lemma, one of many". Groups and analysis. London Math. Soc. Lecture Note Ser. 354. Cambridge: Cambridge Univ. Press. pp. 164–173. MR 2528466.
  3. ↑ François Treves, "Introduction to pseudodifferential and Fourier integral operators", vol. 1, Plenum Press, New York, 1980.