Holdover in synchronization applications
“Synchronization is as important as power at the cell site.”[1]
The quote above suggests that we can think of holdover in synchronization applications as analogous to running on backup power.
Modern wireless communication systems require at least knowledge of frequency and often knowledge of phase as well in order to work correctly. Base stations need to know what time it is, and they usually get this knowledge from the outside world somehow (from a GPS Time and Frequency receiver, or from a synchronization source somewhere in the network they are connected to).
But if the connection to the reference is lost then the base station will be on its own to establish what time it is. The base station needs a way to establish accurate frequency and phase (to know what time it is) using internal (or local) resources, and that’s where the function of holdover becomes important.
Two independent clocks, once synchronized, will walk away from one another without limit.[2] To have them display the same time it would be necessary to re-synchronize them at regular intervals. The periods between synchronizations is referred to as Holdover and performance under Holdover relies on the quality of the reference oscillator (usually an OCXO), the PLL design and the correction mechanisms employed.[3]
The Importance of GPS Derived Timing
A key application for GPS in telecommunications is to provide synchronization in wireless basestations. Base stations depend on timing to operate correctly, particularly for the handoff that occurs when a user moves from one cell to another.[4] In these applications holdover is used in base stations to ensure continued operation while GPS is unavailable and to reduce the costs associated with emergency repairs, since holdover allows the site to continue to function correctly until maintenance can be performed at a convenient time.[5]
Some of the most stringent requirements come from the newer generation of wireless base stations, where phase accuracy targets as low as 1μs need to be maintained for correct operation.[6] However the need for accurate timing has been an integral part of the history of wireless communication systems as well as wireline,[7] and it has been suggested that the search for reliable and cost effective timing solutions was spurred on by the need for CDMA to compete with lower cost solutions.[8]
Within the base station, besides standard functions, accurate timing and the means to maintain it through holdover is vitally important for services such as E911[5]
GPS as a source of timing is a key component in not just Synchronization in telecommunications but to critical infrastructure in general.[9] Of the 18 Critical Resource and Key infrastructure (CIKR[10])sectors, 15 use GPS derived timing to function correctly.[11] One notable application where highly accurate timing accuracy (and the means to maintain it through holdover) is of importance is in the use of Synchrophasors in the power industry to detect line faults.[12] Another is in Low latency trading applications in capital markets.
How GPS Derived Timing Can Fail
GPS is sensitive to jamming and interference because the signal levels the system levels are so low[13] and can easily be swamped by other sources, that can be accidental or deliberate.[14] Also since GPS depends on line of sight signals it can be disrupted by Urban canyon effects, making GPS only available to some locations at certain times of the day, for example.
A GPS outage however is not initially an issue because clocks can go into holdover,[15] allowing the interference to be alleviated as much as the stability of the oscillator providing holdover will allow.[4] The more stable the oscillator, the longer the system can operate without GPS.
Defining Holdover
In Synchronization in telecommunications applications holdover is defined by ETSI as:
An operating condition of a clock which has lost its controlling input and is using stored data, acquired while in locked operation, to control its output. The stored data are used to control phase and frequency variations, allowing the locked condition to be reproduced within specifications. Holdover begins when the clock output no longer reflects the influence of a connected external reference, or transition from it. Holdover terminates when the output of the clock reverts to locked mode condition.[16]
We can regard Holdover then as a measure of accuracy or error acquired by a clock when there is no controlling external reference to correct for any errors.
MIL-PRF-55310[17] defines Clock Accuracy as:
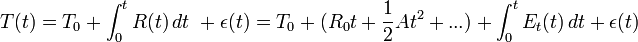
Where 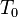 is the synchronization error at
is the synchronization error at 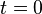 ;
; 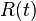 is the fractional frequency difference between two clocks under comparison;
is the fractional frequency difference between two clocks under comparison; 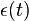 is the error due to random noise;
is the error due to random noise; 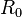 is
is 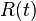 at
at 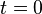 ;
;  is the linear aging rate and
is the linear aging rate and 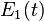 is the frequency difference due to environmental effects.
is the frequency difference due to environmental effects.
Similarly ITU G.810[18] defines Time Error as:
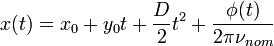
Where 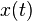 is the time error;
is the time error; 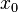 is the time error at
is the time error at 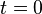 ;
;  is the fractional frequency error at
is the fractional frequency error at 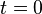 ;
;  is the linear fractional frequency drift rate;
is the linear fractional frequency drift rate; 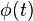 is the random phase deviation component and
is the random phase deviation component and 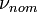 is the nominal frequency.
is the nominal frequency.
Implementing Holdover
In applications that require Synchronization (such as wireless base stations) GPS Clocks are often used and in this context are often known as a GPSDO (GPS Disciplined Oscillator) or GPS TFS (GPS Time and Frequency Source).[19]
NIST defines a Disciplined Oscillator as:
An oscillator whose output frequency is continuously steered (often through the use of a phase locked loop) to agree with an external reference. For example, a GPS disciplined oscillator (GPSDO) usually consists of a quartz or rubidium oscillator whose output frequency is continuously steered to agree with signals broadcast by the GPS satellites.[20]
In a GPSDO a GPS or GNSS signal is used as the external reference that steers an internal oscillator.[13] In a modern GPSDO the GPS processing and steering function are both implemented in a Microprocessor allowing a direct comparison between the GPS reference signal and the oscillator output.[8]

Amongst the building blocks of a GPS Time and Frequency solution the oscillator is a key component[11] and typically they are built around an Oven Controlled Crystal Oscillator (OCXO) or a Rubidium based clock. The dominant factors influencing the quality of the reference oscillator are taken to be aging and temperature stability. However, depending upon the construction of the oscillator, barometric pressure and relative humidity can have at least as strong an influence on the stability of the quartz oscillator. What is often referred to as "random walk" instability is actually a deterministic effect of environmental parameters. These can be measured and modeled to vastly improve the performance of quartz oscillators. An addition of a Microprocessor to the reference oscillator can improve temperature stability and aging performance[21] During Holdover any remaining clock error caused by aging and temperature instability can be corrected by control mechanisms.[22] A combination of quartz based reference oscillator (such as an OCXO) and modern correction algorithms can get good results in Holdover applications.[23]
The Holdover capability then is provided either by a free running local oscillator, or a local oscillator that is steered with software that retains knowledge of its past performance.[23] The earliest documentation of such an effort comes from the then National Bureau of Standards in 1968 [Allan, Fey, Machlan and Barnes, "An Ultra Precise Time Synchronization System Designed By Computer Simulation", Frequency], where an analog computer consisting of ball-disk integrators implemented a third order control loop to correct for the frequency ageing of an oscillator. The first microprocessor implementation of this concept occurred in 1983 [Bourke, Penrod, "An Analysis of a Microprocessor Controlled Disciplined Frequency Standard", Frequency Control Symposium] where Loran-C broadcasts were used to discipline very high quality quartz oscillators as a Cesium replacement in telecommunications wireline network synchronization. The basic aim of a steering mechanism is to improve the stability of a clock or oscillator while minimizing the number of times it needs calibration[24] In Holdover the learned behaviour of the OCXO is used to anticipate and correct for future behavior[3] Effective aging and temperature compensation can be provided by such a mechanism[25] and the system designer is faced with a range of choices for algorithms and techniques to do this correction including extrapolation, interpolation and predictive filters (including Kalman filters).[26][27]
Once the barriers of aging and environmental effects are removed the only theoretical limitation to holdover performance in such a GPSDO is irregularity or noise in the drift rate, which is quantified using a metric like Allan deviation or Time deviation.[28]
The complexity in trying to predict the effects on Holdover due to systematic effects like aging and temperature stability and stochastic influences like Random Walk noise has resulted in tailor-made Holdover Oscillator solutions being introduced in the market.[29]
See also
- Synchronization
- Synchronization in Synchronous optical networking
- Time transfer
- Timekeeping in Global Positioning System
- Precision Time Protocol
References
- ↑ "Synchronization Deployment Considerations for IP RAN Backhaul Operators". Juniper Networks. 2011. Retrieved 2012-10-21.
- ↑ "Smart Clock: A New Time". IEEE. 1992-12-06. Retrieved 2012-10-21.
- ↑ 3.0 3.1 "AN-1002 (Rev. 0)" (PDF). Retrieved 2012-09-28.
- ↑ 4.0 4.1 Faisal A. Khan (December 2007). "Impacts of GPS-Based Synchronization Degradation on Cellular Networks". IGNSS. Retrieved 2012-10-21.
- ↑ 5.0 5.1 "Understanding the concepts of synchronization and holdover". Eetimes.com. Retrieved 2012-09-28.
- ↑
- ↑ "Clocks for the Synchronized Network". Retrieved 2012-10-21.
- ↑ 8.0 8.1 Peter Kuykendall; Dr. Peter V. W. Loomis. "In Sync with GPS: GPS Clocks for the Wireless Infrastructure". Retrieved 2012-10-21.
- ↑ Dr. James Carroll; Mr. Kirk Montgomery. "Global Positioning System Timing Criticality Assessment - Preliminary Performance Results". Retrieved 2012-10-21.
- ↑ http://training.fema.gov/EMIWeb/IS/IS860a/CIKR/sectorMenu.htm
- ↑ 11.0 11.1 R. James Caverly (2011-04-27). "GPS Critical Infrastructure". Retrieved 2012-10-21.
- ↑ "Signal" (PDF). Retrieved 2012-09-28.
- ↑ 13.0 13.1 "The Global Positioning System (GPS)� and �Satellite Time Transfer". March 2010. Retrieved 2012-10-21.
- ↑ "GPS.gov: National Space-Based Positioning, Navigation, and Timing Advisory Board". Pnt.gov. 2012-08-21. Retrieved 2012-09-28.
- ↑ "Sync University". Sync University. 2004-12-15. Retrieved 2012-09-28.
- ↑ "ETS 300 462-1 - Edition 01 - Transmission and Multiplexing (TM); Generic requirements for synchronization networks; Part 1: Definitions and terminology for synchronization networks" (PDF). Retrieved 2012-09-28.
- ↑
- ↑ tsbmail. "G.810 : Definitions and terminology for synchronization networks". Itu.int. Retrieved 2012-09-28.
- ↑ "GPS Time and Frequency Systems". Retrieved 2012-10-21.
- ↑ "Time and Frequency from A to Z". Tf.nist.gov. Retrieved 2012-09-28.
- ↑ "IEEE Xplore - Improvements in OCXO performance by the use of an on-board microprocessor". Ieeexplore.ieee.org. doi:10.1109/FREQ.2008.4622980. Retrieved 2012-09-28.
- ↑ Hui Zhou, Charles Nicholls, Thomas Kunz, Howard Schwartz (November 2008). "Frequency Accuracy & Stability Dependencies of Crystal Oscillators". Retrieved 2012-10-21.
- ↑ 23.0 23.1 Michael A. Lombardi (September 2008). "The Use of GPS Disciplined Oscillators as Primary Frequency Standards for Calibration and Metrology Laboratories". NCSL International. Retrieved 2012-10-21.
- ↑ "IEEE Xplore - Smart clock: a new time". Ieeexplore.ieee.org. 2011-09-27. doi:10.1109/19.199433. Retrieved 2012-09-28.
- ↑ Fabrizio Tappero; Andrew G. Dempster; Toshiaki Iwata (2007). "Phase error reduction method for free-run QZSS clock". IEEE. Retrieved 2012-10-21.
- ↑
- ↑ "IEEE Xplore - Adaptive OCXO drift correction algorithm". Ieeexplore.ieee.org. doi:10.1109/FREQ.2004.1418510. Retrieved 2012-09-28.
- ↑ http://www.leapsecond.com/pages/adev/adev-why.htm
- ↑ "MD-023: Extended Holdover Crystal Oscillator". Vectron International. June 2011. Retrieved 2012-10-21.