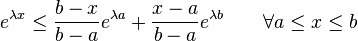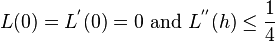Hoeffding's lemma

In probability theory, Hoeffding's lemma is an inequality that bounds the moment-generating function of any bounded random variable. It is named after the Finnish–American mathematical statistician Wassily Hoeffding.

The proof of Hoeffding's lemma uses Taylor's theorem and Jensen's inequality. Hoeffding's lemma is itself used in the proof of McDiarmid's inequality.

Statement of the lemma

Let X be any real-valued random variable with expected value E[X] = 0 and such that a ≤ X ≤ b almost surely. Then, for all λ ∈ R,

\mathbf{E} \left[ e^{\lambda X} \right] \leq \exp \left( \frac{\lambda^2 (b - a)^2}{8} \right).

Proof of the lemma

Since 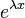e^{\lambda x} is a convex function of x, we have

e^{\lambda x}\leq \frac{b-x}{b-a}e^{\lambda a}+\frac{x-a}{b-a}e^{\lambda b}\qquad \forall a\leq x\leq b

So, \mathbf{E}\left[e^{\lambda X}\right] \leq \frac{b-EX}{b-a}e^{\lambda a}+\frac{EX-a}{b-a}e^{\lambda b}.

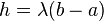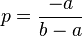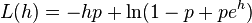
Let h=\lambda(b-a), p=\frac{-a}{b-a} and L(h)=-hp+\ln(1-p+pe^h)

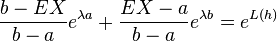Then, \frac{b-EX}{b-a}e^{\lambda a}+\frac{EX-a}{b-a}e^{\lambda b}=e^{L(h)} since EX=0

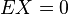
Taking derivative of 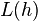L(h),

L(0)=L^{'}(0)=0\text{ and } L^{''}(h)\leq \frac{1}{4}

By Taylor's expansion,

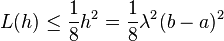
L(h)\leq \frac{1}{8}h^2=\frac{1}{8}\lambda^2(b-a)^2

Hence, \mathbf{E}\left[e^{\lambda X}\right] \leq e^{\frac{1}{8}\lambda^2(b-a)^2}

See also