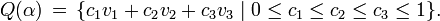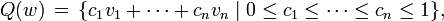Hill tetrahedron
In geometry, the Hill tetrahedra are a family of space-filling tetrahedra. They were discovered in 1896 by M. J. M. Hill, a professor of mathematics at the University College London, who showed that they are scissor-congruent to a cube.
Construction
For every 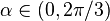 , let
, let 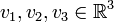 be three unit vectors with angle
be three unit vectors with angle  between every two of them.
Define the Hill tetrahedron
between every two of them.
Define the Hill tetrahedron 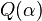 as follows:
as follows:
A special case 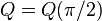 is the tetrahedron having all sides right triangles with sides 1,
is the tetrahedron having all sides right triangles with sides 1, 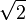 and
and 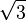 . Ludwig Schläfli studied
. Ludwig Schläfli studied 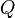 as a special case of the orthoscheme, and H. S. M. Coxeter called it the characteristic tetrahedron of the cubic spacefilling.
as a special case of the orthoscheme, and H. S. M. Coxeter called it the characteristic tetrahedron of the cubic spacefilling.
Properties
- A cube can be tiled with 6 copies of
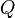 .
. - Every
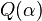 can be dissected into three polytopes which can be reassembled into a prism.
can be dissected into three polytopes which can be reassembled into a prism.
Generalizations
In 1951 Hugo Hadwiger found the following n-dimensional generalization of Hill tetrahedra:
where vectors 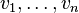 satisfy
satisfy 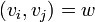 for all
for all 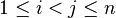 , and where
, and where 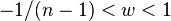 . Hadwiger showed that all such simplices are scissor congruent to a hypercube.
. Hadwiger showed that all such simplices are scissor congruent to a hypercube.
See also
References
- M. J. M. Hill, Determination of the volumes of certain species of tetrahedra without employment of the method of limits, Proc. London Math. Soc., 27 (1895–1896), 39–53.
- H. Hadwiger, Hillsche Hypertetraeder, Gazeta Matemática (Lisboa), 12 (No. 50, 1951), 47–48.
- H.S.M. Coxeter, Frieze patterns, Acta Arithmetica 18 (1971), 297–310.
- E. Hertel, Zwei Kennzeichnungen der Hillschen Tetraeder, J. Geom. 71 (2001), no. 1–2, 68–77.
- Greg N. Frederickson, Dissections: Plane and Fancy, Cambridge University Press, 2003.
- N.J.A. Sloane, V.A. Vaishampayan, Generalizations of Schobi’s Tetrahedral Dissection, arXiv:0710.3857.