Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u(t), and produces a function, H(u)(t), with the same domain. The Hilbert transform is important in the field of signal processing where it is used to derive the analytic representation of a signal u(t). This means that real signal u(t) is extended into the complex plane such that it satisfies the Cauchy-Riemann equations. For example, the Hilbert transform leads to the harmonic conjugate of a given function in Fourier analysis, aka harmonic analysis. Equivalently, it is an example of a singular integral operator and of a Fourier multiplier.
The Hilbert transform was originally defined for periodic functions, or equivalently for functions on the circle, in which case it is given by convolution with the Hilbert kernel. More commonly, however, the Hilbert transform refers to a convolution with the Cauchy kernel, for functions defined on the real line R (the boundary of the upper half-plane). The Hilbert transform is closely related to the Paley–Wiener theorem, another result relating holomorphic functions in the upper half-plane and Fourier transforms of functions on the real line.
The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the Riemann–Hilbert problem for holomorphic functions.

Introduction
The Hilbert transform of u can be thought of as the convolution of u(t) with the function h(t) = 1/(πt). Because h(t) is not integrable, the integrals defining the convolution do not converge. Instead, the Hilbert transform is defined using the Cauchy principal value (denoted here by p.v.). Explicitly, the Hilbert transform of a function (or signal) u(t) is given by:
provided this integral exists as a principal value. This is precisely the convolution of u with the tempered distribution p.v. 1/πt (due to Schwartz (1950); see Pandey (1996, Chapter 3)). Alternatively, by changing variables, the principal value integral can be written explicitly (Zygmund 1968, §XVI.1) as:
When the Hilbert transform is applied twice in succession to a function u, the result is negative u:
provided the integrals defining both iterations converge in a suitable sense. In particular, the inverse transform is −H. This fact can most easily be seen by considering the effect of the Hilbert transform on the Fourier transform of u(t) (see Relationship with the Fourier transform, below).
For an analytic function in upper half-plane, the Hilbert transform describes the relationship between the real part and the imaginary part of the boundary values. That is, if f(z) is analytic in the plane Im z > 0 and u(t) = Re f(t + 0·i ) then Im f(t + 0·i ) = H(u)(t) up to an additive constant, provided this Hilbert transform exists.
Notation
In signal processing the Hilbert transform of u(t) is commonly denoted by 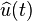 (e.g., Brandwood 2003, pg 87). However, in mathematics, this notation is already extensively used to denote the Fourier transform of u(t) (e.g., Stein & Weiss 1971). Occasionally, the Hilbert transform may be denoted by
(e.g., Brandwood 2003, pg 87). However, in mathematics, this notation is already extensively used to denote the Fourier transform of u(t) (e.g., Stein & Weiss 1971). Occasionally, the Hilbert transform may be denoted by 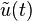 . Furthermore, many sources define the Hilbert transform as the negative of the one defined here (e.g., Bracewell 2000, pg 359).
. Furthermore, many sources define the Hilbert transform as the negative of the one defined here (e.g., Bracewell 2000, pg 359).
History
The Hilbert transform arose in Hilbert's 1905 work on a problem posed by Riemann concerning analytic functions (Kress (1989); Bitsadze (2001)) which has come to be known as the Riemann–Hilbert problem. Hilbert's work was mainly concerned with the Hilbert transform for functions defined on the circle (Khvedelidze 2001; Hilbert 1953). Some of his earlier work related to the Discrete Hilbert Transform dates back to lectures he gave in Göttingen. The results were later published by Hermann Weyl in his dissertation (Hardy, Littlewood & Polya 1952, §9.1). Schur improved Hilbert's results about the discrete Hilbert transform and extended them to the integral case (Hardy, Littlewood & Polya 1952, §9.2). These results were restricted to the spaces L2 and ℓ2. In 1928, Marcel Riesz proved that the Hilbert transform can be defined for u in Lp(R) for 1 ≤ p < ∞, that the Hilbert transform is a bounded operator on Lp(R) for 1 < p < ∞, and that similar results hold for the Hilbert transform on the circle as well as the discrete Hilbert transform (Riesz 1928). The Hilbert transform was a motivating example for Antoni Zygmund and Alberto Calderón during their study of singular integrals (Calderón & Zygmund 1952). Their investigations have played a fundamental role in modern harmonic analysis. Various generalizations of the Hilbert transform, such as the bilinear and trilinear Hilbert transforms are still active areas of research today.
Relationship with the Fourier transform
The Hilbert transform is a multiplier operator (Duoandikoetxea 2000, Chapter 3). The symbol of H is σH(ω) = −i sgn(ω) where sgn is the signum function. Therefore:
where  denotes the Fourier transform. Since sgn(x) = sgn(2πx), it follows that this result applies to the three common definitions of
denotes the Fourier transform. Since sgn(x) = sgn(2πx), it follows that this result applies to the three common definitions of  .
.
By Euler's formula,
Therefore H(u)(t) has the effect of shifting the phase of the negative frequency components of u(t) by +90° (π/2 radians) and the phase of the positive frequency components by −90°. And i·H(u)(t) has the effect of restoring the positive frequency components while shifting the negative frequency ones an additional +90°, resulting in their negation.
When the Hilbert transform is applied twice, the phase of the negative and positive frequency components of u(t) are respectively shifted by +180° and −180°, which are equivalent amounts. The signal is negated; i.e., H(H(u)) = −u, because:
Table of selected Hilbert transforms
Signal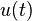 | Hilbert transform[fn 1]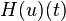 |
|---|---|
 [fn 2] [fn 2] | 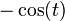 |
 [fn 2] [fn 2] |  |
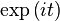 |  |
 | 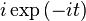 |
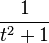 |  |
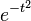 |  see Dawson function see Dawson function |
Sinc function 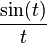 | 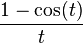 |
Rectangular function 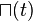 |  |
Dirac delta function 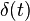 |  |
Characteristic Function ![\chi_{[a,b]}(t) \,](../I/m/48958b1f5fb840c34088bf6a3c9974d4.png) | 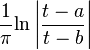 |
- Notes
- ↑ Some authors (e.g., Bracewell) use our −H as their definition of the forward transform. A consequence is that the right column of this table would be negated.
- ↑ 2.0 2.1 The Hilbert transform of the sin and cos functions can be defined in a distributional sense, if there is a concern that the integral defining them is otherwise conditionally convergent. In the periodic setting this result holds without any difficulty.
An extensive table of Hilbert transforms is available (King 2009). Note that the Hilbert transform of a constant is zero.
Domain of definition
It is by no means obvious that the Hilbert transform is well-defined at all, as the improper integral defining it must converge in a suitable sense. However, the Hilbert transform is well-defined for a broad class of functions, namely those in Lp(R) for 1< p <∞.
More precisely, if u is in Lp(R) for 1<p<∞, then the limit defining the improper integral
exists for almost every t. The limit function is also in Lp(R) and is in fact the limit in the mean of the improper integral as well. That is,
as ε→0 in the Lp-norm, as well as pointwise almost everywhere, by the Titchmarsh theorem (Titchmarsh 1948, Chapter 5).
In the case p=1, the Hilbert transform still converges pointwise almost everywhere, but may fail to be itself integrable even locally (Titchmarsh 1948, §5.14). In particular, convergence in the mean does not in general happen in this case. The Hilbert transform of an L1 function does converge, however, in L1-weak, and the Hilbert transform is a bounded operator from L1 to L1,w (Stein & Weiss 1971, Lemma V.2.8). (In particular, since the Hilbert transform is also a multiplier operator on L2, Marcinkiewicz interpolation and a duality argument furnishes an alternative proof that H is bounded on Lp.)
Properties
Boundedness
If 1<p<∞, then the Hilbert transform on Lp(R) is a bounded linear operator, meaning that there exists a constant Cp such that
for all u∈Lp(R). This theorem is due to Riesz (1928, VII); see also Titchmarsh (1948, Theorem 101). The best constant Cp is given by
This result is due to (Pichorides 1972); see also Grafakos (2004, Remark 4.1.8). The same best constants hold for the periodic Hilbert transform.
The boundedness of the Hilbert transform implies the Lp(R) convergence of the symmetric partial sum operator
to f in Lp(R), see for example (Duoandikoetxea 2000, p. 59).
Anti-self adjointness
The Hilbert transform is an anti-self adjoint operator relative to the duality pairing between Lp(R) and the dual space Lq(R), where p and q are Hölder conjugates and 1 < p,q < ∞. Symbolically,
for u ∈ Lp(R) and v ∈ Lq(R) (Titchmarsh 1948, Theorem 102).
Inverse transform
The Hilbert transform is an anti-involution (Titchmarsh 1948, p. 120), meaning that
provided each transform is well-defined. Since H preserves the space Lp(R), this implies in particular that the Hilbert transform is invertible on Lp(R), and that
Differentiation
Formally, the derivative of the Hilbert transform is the Hilbert transform of the derivative, i.e. these two linear operators commute:
Iterating this identity,
This is rigorously true as stated provided u and its first k derivatives belong to Lp(R) (Pandey 1996, §3.3). One can check this easily in the frequency domain, where differentiation becomes multiplication by ω.
Convolutions
The Hilbert transform can formally be realized as a convolution with the tempered distribution (Duistermaat & Kolk 2010, p. 211)
Thus formally,
However, a priori this may only be defined for u a distribution of compact support. It is possible to work somewhat rigorously with this since compactly supported functions (which are distributions a fortiori) are dense in Lp. Alternatively, one may use the fact that h(t) is the distributional derivative of the function log|t|/π; to wit
For most operational purposes the Hilbert transform can be treated as a convolution. For example, in a formal sense, the Hilbert transform of a convolution is the convolution of the Hilbert transform on either factor:
This is rigorously true if u and v are compactly supported distributions since, in that case,
By passing to an appropriate limit, it is thus also true if u ∈ Lp and v ∈ Lr provided
a theorem due to Titchmarsh (1948, Theorem 104).
Invariance
The Hilbert transform has the following invariance properties on L2(R).
- It commutes with translations. That is, it commutes with the operators Taƒ(x) = ƒ(x + a) for all a in R
- It commutes with positive dilations. That is it commutes with the operators Mλƒ(x) = ƒ(λx) for all λ > 0.
- It anticommutes with the reflection Rƒ(x) = ƒ(−x).
Up to a multiplicative constant, the Hilbert transform is the only bounded operator on L2 with these properties (Stein 1970, §III.1).
In fact there is a larger group of operators commuting with the Hilbert transform. The group SL(2,R) acts by unitary operators Ug on the space L2(R) by the formula
This unitary representation is an example of a principal series representation of SL(2,R). In this case it is reducible, splitting as the orthogonal sum of two invariant subspaces, Hardy space H2(R) and its conjugate. These are the spaces of L2 boundary values of holomorphic functions on the upper and lower halfplanes. H2(R) and its conjugate consist of exactly those L2 functions with Fourier transforms vanishing on the negative and positive parts of the real axis respectively. Since the Hilbert transform is equal to H = -i (2P - I), with P being the orthogonal projection from L2(R) onto H2(R), it follows that H2(R) and its orthogonal are eigenspaces of H for the eigenvalues ± i. In other words H commutes with the operators Ug. The restrictions of the operators Ug to H2(R) and its conjugate give irreducible representations of SL(2,R)—the so-called limit of discrete series representations.[1]
Extending the domain of definition
Hilbert transform of distributions
It is further possible to extend the Hilbert transform to certain spaces of distributions (Pandey 1996, Chapter 3). Since the Hilbert transform commutes with differentiation, and is a bounded operator on Lp, H restricts to give a continuous transform on the inverse limit of Sobolev spaces:
The Hilbert transform can then be defined on the dual space of 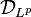 , denoted
, denoted 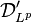 , consisting of Lp distributions. This is accomplished by the duality pairing: for
, consisting of Lp distributions. This is accomplished by the duality pairing: for 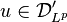 , define
, define 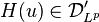 by
by
for all 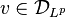 .
.
It is possible to define the Hilbert transform on the space of tempered distributions as well by an approach due to Gel'fand & Shilov (1967), but considerably more care is needed because of the singularity in the integral.
Hilbert transform of bounded functions
The Hilbert transform can be defined for functions in L∞(R) as well, but it requires some modifications and caveats. Properly understood, the Hilbert transform maps L∞(R) to the Banach space of bounded mean oscillation (BMO) classes.
Interpreted naively, the Hilbert transform of a bounded function is clearly ill-defined. For instance, with u = sgn(x), the integral defining H(u) diverges almost everywhere to ±∞. To alleviate such difficulties, the Hilbert transform of an L∞-function is therefore defined by the following regularized form of the integral
where as above h(x) = 1/πx and
The modified transform H agrees with the original transform on functions of compact support by a general result of Calderón & Zygmund (1952); see Fefferman (1971). The resulting integral, furthermore, converges pointwise almost everywhere, and with respect to the BMO norm, to a function of bounded mean oscillation.
A deep result of Fefferman (1971) and Fefferman & Stein (1972) is that a function is of bounded mean oscillation if and only if it has the form ƒ + H(g) for some ƒ, g ∈ L∞(R).
Conjugate functions
The Hilbert transform can be understood in terms of a pair of functions f(x) and g(x) such that the function
is the boundary value of a holomorphic function F(z) in the upper half-plane (Titchmarsh 1948, Chapter V). Under these circumstances, if f and g are sufficiently integrable, then one is the Hilbert transform of the other.
Suppose that f ∈ Lp(R). Then, by the theory of the Poisson integral, f admits a unique harmonic extension into the upper half-plane, and this extension is given by
which is the convolution of f with the Poisson kernel
Furthermore, there is a unique harmonic function v defined in the upper half-plane such that F(z) = u(z) + iv(z) is holomorphic and
This harmonic function is obtained from f by taking a convolution with the conjugate Poisson kernel
Thus
Indeed, the real and imaginary parts of the Cauchy kernel are
so that F = u + iv is holomorphic by Cauchy's integral formula.
The function v obtained from u in this way is called the harmonic conjugate of u. The (non-tangential) boundary limit of v(x,y) as y → 0 is the Hilbert transform of f. Thus, succinctly,
Titchmarsh's theorem
A theorem due to Edward Charles Titchmarsh makes precise the relationship between the boundary values of holomorphic functions in the upper half-plane and the Hilbert transform (Titchmarsh 1948, Theorem 95). It gives necessary and sufficient conditions for a complex-valued square-integrable function F(x) on the real line to be the boundary value of a function in the Hardy space H2(U) of holomorphic functions in the upper half-plane U.
The theorem states that the following conditions for a complex-valued square-integrable function F : R → C are equivalent:
- F(x) is the limit as z → x of a holomorphic function F(z) in the upper half-plane such that
- The real and imaginary parts of the Fourier transform of F(x) are Hilbert transforms of each other.
- The Fourier transform
 vanishes for x < 0.
vanishes for x < 0.
A weaker result is true for functions of class Lp for p > 1 (Titchmarsh 1948, Theorem 103). Specifically, if F(z) is a holomorphic function such that
for all y, then there is a complex-valued function F(x) in Lp(R) such that F(x + iy) → F(x) in the Lp norm as y → 0 (as well as holding pointwise almost everywhere). Furthermore,
where ƒ is a real-valued function in Lp(R) and g is the Hilbert transform (of class Lp) of ƒ.
This is not true in the case p = 1. In fact, the Hilbert transform of an L1 function ƒ need not converge in the mean to another L1 function. Nevertheless (Titchmarsh 1948, Theorem 105), the Hilbert transform of ƒ does converge almost everywhere to a finite function g such that
This result is directly analogous to one by Andrey Kolmogorov for Hardy functions in the disc (Duren 1970, Theorem 4.2).
Riemann–Hilbert problem
One form of the Riemann–Hilbert problem seeks to identify pairs of functions F+ and F− such that F+ is holomorphic on the upper half-plane and F− is holomorphic on the lower half-plane, such that for x along the real axis,
where f(x) is some given real-valued function of x ∈ R. The left-hand side of this equation may be understood either as the difference of the limits of F± from the appropriate half-planes, or as a hyperfunction distribution. Two functions of this form are a solution of the Riemann–Hilbert problem.
Formally, if F± solve the Riemann–Hilbert problem
then the Hilbert transform of f(x) is given by
 (Pandey 1996, Chapter 2).
(Pandey 1996, Chapter 2).
Hilbert transform on the circle
For a periodic function f the circular Hilbert transform is defined as
The circular Hilbert transform is used in giving a characterization of Hardy space and in the study of the conjugate function in Fourier series. The kernel,
 is known as the Hilbert kernel since it was in this form the Hilbert transform was originally studied (Khvedelidze 2001).
is known as the Hilbert kernel since it was in this form the Hilbert transform was originally studied (Khvedelidze 2001).
The Hilbert kernel (for the circular Hilbert transform) can be obtained by making the Cauchy kernel 1/x periodic. More precisely, for x≠0
Many results about the circular Hilbert transform may be derived from the corresponding results for the Hilbert transform from this correspondence.
Another more direct connection is provided by the Cayley transform C(x) = (x – i) / (x + i), which carries the real line onto the circle and the upper half plane onto the unit disk. It induces a unitary map
of L2(T) onto L2(R). The operator U carries the Hardy space H2(T) onto the Hardy space H2(R).[2]
Hilbert transform in signal processing
Bedrosian's theorem
Bedrosian's theorem states that the Hilbert transform of the product of a low-pass and a high-pass signal with non-overlapping spectra is given by the product of the low-pass signal and the Hilbert transform of the high-pass signal, or
where fLP and fHP are the low- and high-pass signals respectively (Schreier & Scharf 2010, 14).
Amplitude modulated signals are modeled as the product of a bandlimited "message" waveform, um(t), and a sinusoidal "carrier":
When um(t) has no frequency content above the carrier frequency, 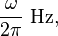 then by Bedrosian's theorem:
then by Bedrosian's theorem:
Analytic representation
In the context of signal processing, the conjugate function interpretation of the Hilbert transform, discussed above, gives the analytic representation of a signal u(t):
which is a holomorphic function in the upper half plane.
For the narrowband model [above], the analytic representation is:
-
 (by Euler's formula)
(by Euler's formula)(Eq.1)
-
This complex heterodyne operation shifts all the frequency components of um(t) above 0 Hz. In that case, the imaginary part of the result is a Hilbert transform of the real part. This is an indirect way to produce Hilbert transforms.
Phase/frequency modulation
The form:
is called phase (or frequency) modulation. The instantaneous frequency is  For sufficiently large ω, compared to
For sufficiently large ω, compared to  :
:
and:
Single sideband modulation (SSB)
When um(t) in Eq.1 is also an analytic representation (of a message waveform), that is:
the result is single-sideband modulation:
whose transmitted component is:
Causality
The function h with h(t) = 1/(πt) is a non-causal filter and therefore cannot be implemented as is, if u is a time-dependent signal. If u is a function of a non-temporal variable (e.g., spatial) the non-causality might not be a problem. The filter is also of infinite support which may be a problem in certain applications. Another issue relates to what happens with the zero frequency (DC), which can be avoided by assuring that s does not contain a DC-component.
A practical implementation in many cases implies that a finite support filter, which in addition is made causal by means of a suitable delay, is used to approximate the computation. The approximation may also imply that only a specific frequency range is subject to the characteristic phase shift related to the Hilbert transform. See also quadrature filter.
Discrete Hilbert transform





For a discrete function, ![u[n],](../I/m/472c10e057e3a707f0af696702689a74.png) with discrete-time Fourier transform (DTFT),
with discrete-time Fourier transform (DTFT),  and discrete Hilbert transform
and discrete Hilbert transform ![\hat u[n],](../I/m/8d39c632d32b8025db3fa756ac83c32c.png) the DTFT of
the DTFT of ![\hat u[n]](../I/m/8571f35418962cf1bd5e6ad4911c18a3.png) in the region -π < ω < π is given by:
in the region -π < ω < π is given by:
The inverse DTFT, using the convolution theorem, is:
where:
which is an infinite impulse response (IIR). When the convolution is performed numerically, an FIR approximation is substituted for h[n], as shown in Figure 1. An FIR filter with an odd number of anti-symmetric coefficients is called Type III, which inherently exhibits responses of zero magnitude at frequencies 0 and Nyquist, resulting in this case in a bandpass filter shape. A Type IV design (even number of anti-symmetric coefficients) is shown in Figure 2. Since the magnitude response at Nyquist does not drop out, it approximates an ideal Hilbert transformer a little better than the odd-tap filter. However:
- A typical (i.e. properly filtered and sampled) u[n] sequence has no useful components at the Nyquist frequency.
- The Type IV impulse response requires a ½ sample shift in the h[n] sequence. That causes the zero-valued coefficients to become non-zero, as seen in Figure 2. So a Type III design is potentially twice as efficient as Type IV.
- The group delay of a Type III design is an integer number of samples, which facilitates aligning
![\hat u[n]](../I/m/8571f35418962cf1bd5e6ad4911c18a3.png) with
with ![u[n],](../I/m/472c10e057e3a707f0af696702689a74.png) to create an analytic signal. The group delay of Type IV is halfway between two samples.
to create an analytic signal. The group delay of Type IV is halfway between two samples.
With an FIR approximation to h[n], denoted below by ![\tilde{h}[n],](../I/m/e59d23fb9859207669f49cdd79c07328.png) a method called overlap-save is often used to perform the convolution on a long u[n] sequence. Segments of length N are convolved with the M filter coefficients, where N > M, resulting in N-M+1 samples of
a method called overlap-save is often used to perform the convolution on a long u[n] sequence. Segments of length N are convolved with the M filter coefficients, where N > M, resulting in N-M+1 samples of 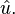 The usual implementation actually convolves the u[n] segments with the periodic summation:[3]
The usual implementation actually convolves the u[n] segments with the periodic summation:[3]
which only affects the values of the M-1 outputs that are discarded from each block of N. A tempting shortcut in that implementation is to substitute samples of -i•sgn(ω) (whose real and imaginary components are all just 0 or ±1) for the array FFT That has the effect of convolving with the periodic summation of h[n]. Figure 3 compares a half-cycle of hN[n] with an equivalent length portion of h[n]. Figure 4 is an example of using both the FIR approximation and the DTFT samples. In the example, a sine function is created by computing the Discrete Hilbert transform of a cosine function, which was processed in 4 overlapping segments, and pieced back together. As the FIR result (blue) shows, the distortions apparent in the DTFT result (red) are not caused by the difference between h[n] and hN[n] (green and red in Fig 3). The fact that hN[n] is tapered (windowed) is actually helpful in this context. The real problem is that it's not windowed enough. Effectively, M=N, whereas the overlap-save method needs M < N.
That has the effect of convolving with the periodic summation of h[n]. Figure 3 compares a half-cycle of hN[n] with an equivalent length portion of h[n]. Figure 4 is an example of using both the FIR approximation and the DTFT samples. In the example, a sine function is created by computing the Discrete Hilbert transform of a cosine function, which was processed in 4 overlapping segments, and pieced back together. As the FIR result (blue) shows, the distortions apparent in the DTFT result (red) are not caused by the difference between h[n] and hN[n] (green and red in Fig 3). The fact that hN[n] is tapered (windowed) is actually helpful in this context. The real problem is that it's not windowed enough. Effectively, M=N, whereas the overlap-save method needs M < N.
The popular MATLAB function, hilbert(u,N), returns an approximate discrete Hilbert transform of u[n] in the imaginary part of the complex output sequence. The real part is the original input sequence, so that the complex output is an analytic representation of u[n]. Similar to the discussion above, hilbert(u, N) only uses samples of the sgn(ω) distribution and therefore convolves with hN[n]. The red graph in Figure 5 is the difference between a sine function and the convolution of h256[n] with 256 samples of a cosine function. The durations of the edge effects are essentially the rise and fall times of the h[n] impulse response. The amplitude of the edge effects can be reduced about 50% by increasing N, as shown in the blue graph.
Number Theoretic Hilbert transform
The number theoretic Hilbert transform is an extension (Kak 1970) of the discrete Hilbert transform to integers modulo an appropriate prime number. In this it follows the generalization of discrete Fourier transform to number theoretic transforms. The number theoretic Hilbert transform can be used to generate sets of orthogonal discrete sequences(Kak 2014).
See also
- Analytic signal
- Harmonic conjugate
- Hilbert spectroscopy
- Hilbert transform in the complex plane
- Hilbert–Huang transform
- Kramers–Kronig relation
- Single-sideband signal
- Singular integral operators of convolution type
Notes
- ↑ See:
- ↑ Rosenblum & Rovnyak 1997, p. 92
- ↑ see Convolution Theorem
References
- Bargmann, V. (1947), "Irreducible unitary representations of the Lorentz group", Ann. Of Math. 48 (3): 568–640, doi:10.2307/1969129, JSTOR 1969129
- Bedrosian, E. (December 1962), "A Product Theorem for Hilbert Transforms", Rand Corporation Memorandum (RM-3439-PR)
- Benedetto, John J. (1996). Harmonic analysis and applications. Boca Raton, FL: CRC Press. ISBN 0849378796.
- Bitsadze, A.V. (2001), "Boundary value problems of analytic function theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4.
- Bracewell, R. (1986), The Fourier Transform and Its Applications (2nd ed.), McGraw-Hill, ISBN 0-07-116043-4.
- Calderón, A.P.; Zygmund, A. (1952), "On the existence of certain singular integrals", Acta Mathematica 88 (1): 85–139, doi:10.1007/BF02392130.
- Carlson, Crilly, and Rutledge (2002), Communication Systems (4th ed.), ISBN 0-07-011127-8.
- Duoandikoetxea, J. (2000), Fourier Analysis, American Mathematical Society, ISBN 0-8218-2172-5.
- Duistermaat, J.J.; Kolk, J.A.C. Kolk (2010), Distributions, Birkhäuser, doi:10.1007/978-0-8176-4675-2, ISBN 978-0-8176-4672-1.
- Duren, P. (1970), Theory of
 -Spaces, New York: Academic Press.
-Spaces, New York: Academic Press. - Fefferman, C. (1971), "Characterizations of bounded mean oscillation", Bull. Amer. Math. Soc. 77 (4): 587–588, doi:10.1090/S0002-9904-1971-12763-5, MR 0280994.
- Fefferman, C.; Stein, E.M. (1972), "Hp spaces of several variables", Acta Math. 129: 137–193, doi:10.1007/BF02392215, MR 0447953.
- Gel'fand, I.M.; Shilov, G.E. (1967), Generalized Functions, Vol. 2, Academic Press.
- Grafakos, Loukas (1994), "An Elementary Proof of the Square Summability of the Discrete Hilbert Transform", American Mathematical Monthly (Mathematical Association of America) 101 (5): 456–458, doi:10.2307/2974910, JSTOR 2974910.
- Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Pearson Education, Inc., pp. 253–257, ISBN 0-13-035399-X.
- Hardy, G. H.; Littlewood, J. E.; Polya, G. (1952), Inequalities, Cambridge: Cambridge University Press, ISBN 0-521-35880-9.
- Hilbert, David (1953), Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, Chelsea Pub. Co.
- Kak, Subhash (1970), "The discrete Hilbert transform", Proc. IEEE 58: 585–586 .
- Kak, Subhash (2014), "Number theoretic Hilbert transform", Circuits Systems Signal Processing 33: 2539–2548 .
- Khvedelidze, B.V. (2001), "Hilbert transform", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4.
- King, Frederick W. (2009), Hilbert Transforms 2, Cambridge: Cambridge University Press, p. 453, ISBN 978-0-521-51720-1.
- Kress, Rainer (1989), Linear Integral Equations, New York: Springer-Verlag, p. 91, ISBN 3-540-50616-0.
- Lang, Serge (1985), SL(2,R), Graduate Texts in Mathematics 105, Springer-Verlag, ISBN 0-387-96198-4
- Pandey, J.N. (1996), The Hilbert transform of Schwartz distributions and applications, Wiley-Interscience, ISBN 0-471-03373-1
- Pichorides, S. (1972), "On the best value of the constants in the theorems of Riesz, Zygmund, and Kolmogorov", Studia Mathematica 44: 165–179
- Riesz, Marcel (1928), "Sur les fonctions conjuguées", Mathematische Zeitschrift 27 (1): 218–244, doi:10.1007/BF01171098
- Rosenblum, Marvin; Rovnyak, James (1997), Hardy classes and operator theory, Dover, ISBN 0-486-69536-0
- Schwartz, Laurent (1950), Théorie des distributions, Paris: Hermann.
- Schreier, P.; Scharf, L. (2010), Statistical signal processing of complex-valued data: the theory of improper and noncircular signals, Cambridge University Press
- Stein, Elias (1970), Singular integrals and differentiability properties of functions, Princeton University Press, ISBN 0-691-08079-8.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, ISBN 0-691-08078-X.
- Sugiura, Mitsuo (1990), Unitary Representations and Harmonic Analysis: An Introduction, North-Holland Mathematical Library 44 (2nd ed.), Elsevier, ISBN 0444885935
- Titchmarsh, E (1926), "Reciprocal formulae involving series and integrals", Mathematische Zeitschrift 25 (1): 321–347, doi:10.1007/BF01283842.
- Titchmarsh, E (1948), Introduction to the theory of Fourier integrals (2nd ed.), Oxford University: Clarendon Press (published 1986), ISBN 978-0-8284-0324-5.
- Zygmund, Antoni (1968), Trigonometric series (2nd ed.), Cambridge University Press (published 1988), ISBN 978-0-521-35885-9.
External links
- The Discrete Hilbert Transform; A Brief Tutorial_w236
- Derivation of the boundedness of the Hilbert transform
- Mathworld Hilbert transform — Contains a table of transforms
- Analytic Signals and Hilbert Transform Filters
- Weisstein, Eric W., "Titchmarsh theorem", MathWorld.
- Mathias Johansson, "The Hilbert transform" a student level summary to Hilbert transformation. (via www.archive.org)
- GS256 Lecture 3: Hilbert Transformation, an entry level introduction to Hilbert transformation. (via www.archive.org)
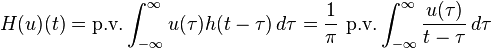


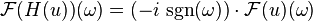


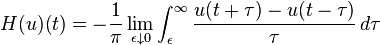
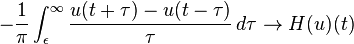







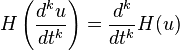
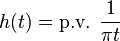



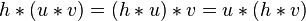


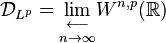
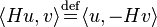

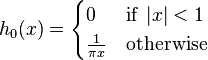
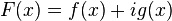


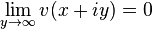
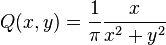


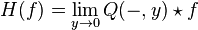
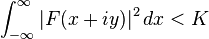
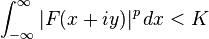



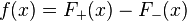

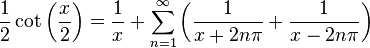

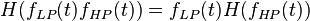
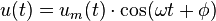
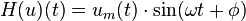
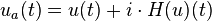


![= u_m(t) \cdot \left[\cos(\omega t + \phi) + i\cdot \sin(\omega t + \phi)\right]](../I/m/8d4bf18e6abcc06395960d2fb4bdead3.png)

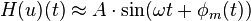
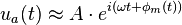

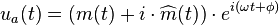


![\begin{align}
\hat u[n] &= \scriptstyle{DTFT}^{-1} \displaystyle (U(\omega))\ *\ \scriptstyle{DTFT}^{-1} \displaystyle (-i\cdot \sgn(\omega))\\
&= u[n]\ *\ \frac{1}{2 \pi}\int_{-\pi}^{\pi} (-i\cdot \sgn(\omega))\cdot e^{i \omega n} d\omega\\
&= u[n]\ *\ \underbrace{\frac{1}{2 \pi}\left[\int_{-\pi}^{0} i\cdot e^{i \omega n} d\omega - \int_{0}^{\pi} i\cdot e^{i \omega n} d\omega \right]}_{h[n]},
\end{align}](../I/m/b61a1e6b8b8291d68f98f9631c87599c.png)
![h[n]\ \stackrel{\mathrm{def}}{=}\
\begin{cases}
0, & \mbox{for }n\mbox{ even}\\
\frac2{\pi n} & \mbox{for }n\mbox{ odd},
\end{cases}](../I/m/a783b6f1b9a3e9c9fc4072f844593745.png)
![\tilde{h}_N[n]\ \stackrel{\text{def}}{=}\ \sum_{m=-\infty}^{\infty} \tilde{h}[n - mN],](../I/m/0e785f1df62fc257d4e4e1a70ad2a0bd.png)