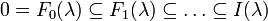Highest-weight category
In the mathematical field of representation theory, a highest-weight category is a k-linear category C (here k is a field) that
- is locally artinian[1]
- has enough injectives
- satisfies
- for all subobjects B and each family of subobjects {Aα} of each object X
and such that there is a locally finite poset Λ (whose elements are called the weights of C) that satisfies the following conditions:[2]
- The poset Λ indexes an exhaustive set of non-isomorphic simple objects {S(λ)} in C.
- Λ also indexes a collection of objects {A(λ)} of objects of C such that there exist embeddings S(λ) → A(λ) such that all composition factors S(μ) of A(λ)/S(λ) satisfy μ < λ.[3]
- For all μ, λ in Λ,
- is finite, and the multiplicity[4]
- is also finite.
- Each S(λ) has an injective envelope I(λ) in C equipped with an increasing filtration
- such that
-
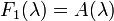
- for n > 1,
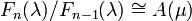 for some μ = μ(n) > λ
for some μ = μ(n) > λ - for each μ in Λ, μ(n) = μ for only finitely many n
-
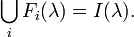
-
Examples
- The module category of the
 -algebra of upper triangular
-algebra of upper triangular 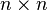 matrices over
matrices over  .
. - This concept is named after the category of highest-weight modules of Lie-algebras.
- A finite-dimensional
 -algebra
-algebra  is quasi-hereditary iff its module category is a highest-weight category. In particular all module-categories over semisimple and hereditary algebras are highest-weight categories.
is quasi-hereditary iff its module category is a highest-weight category. In particular all module-categories over semisimple and hereditary algebras are highest-weight categories. - A cellular algebra over a field is quasi-hereditary (and hence its module category a highest-weight category) iff its Cartan-determinant is 1.
Notes
- ↑ In the sense that it admits arbitrary direct limits of subobjects and every object is a union of its subobjects of finite length.
- ↑ Cline & Scott 1988, §3
- ↑ Here, a composition factor of an object A in C is, by definition, a composition factor of one of its finite length subobjects.
- ↑ Here, if A is an object in C and S is a simple object in C, the multiplicity [A:S] is, by definition, the supremum of the multiplicity of S in all finite length subobjects of A.
References
- Cline, E.; Parshall, B.; Scott, L. (January 1988). "Finite-dimensional algebras and highest-weight categories" (pdf). Journal für die reine und angewandte Mathematik (Berlin, Germany: Walter de Gruyter) 1988 (391): 85–99. doi:10.1515/crll.1988.391.85. ISSN 0075-4102. OCLC 1782270. CiteSeerX: 10
.1 . Retrieved 2012-07-17..1 .112 .6181
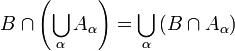
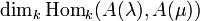
![[A(\lambda):S(\mu)]](../I/m/cde8dd17cdfd7b3ff102393f9f386372.png)