Higher-order derivative test

In mathematics, the higher-order derivative test is used to find maxima, minima, and points of inflection for sufficiently differentiable real-valued functions.

The general derivative test for stationary points

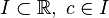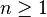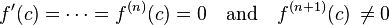
Let $f$ be a real-valued, sufficient differentiable function on the interval $I \subset \R, \; c \in I$ and $n \ge 1$ an integer. If now holds $f'(c)=\cdots=f^{(n)}(c)=0\quad \text{and}\quad f^{(n+1)}(c)\,\not= 0$

then, either

n is odd and we have a local extremum at c. More precisely:

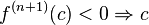$f^{(n+1)}(c)<0 \Rightarrow c$ is a point of a maximum
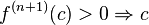$f^{(n+1)}(c)>0 \Rightarrow c$ is a point of a minimum

n is even and we have a (local) saddle point at c. More precisely:

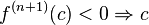$f^{(n+1)}(c)<0 \Rightarrow c$ is a strictly decreasing point of inflection
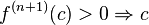$f^{(n+1)}(c)>0 \Rightarrow c$ is a strictly increasing point of inflection

. This analytical test classifies any stationary point of $f$ .

Example

The function 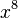$x^8$ has all of its derivatives at 0 equal to 0 except for the 8th derivative, which is positive. Thus, by the test, there is a local minimum at 0.

References

Stewart, James (2008). Calculus: Early Transcendentals, 6th ed., Brooks Cole Cengage Learning. ISBN 978-0-495-01166-8

Higher-order derivative test

The general derivative test for stationary points

Example

See also

References