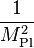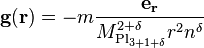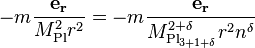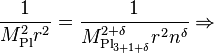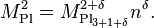Hierarchy problem
| Beyond the Standard Model |
|---|
 Simulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons |
| Standard Model |
In theoretical physics, the hierarchy problem is the large discrepancy between aspects of the weak force and gravity.[1] There is no scientific consensus on, for example, why the weak force is 1032 times stronger than gravity.
Technical definition
A hierarchy problem occurs when the fundamental value of some physical parameter, such as a coupling constant or a mass, in some Lagrangian is vastly different from its effective value, which is the value that gets measured in an experiment. This happens because the effective value is related to the fundamental value by a prescription known as renormalization, which applies quantum corrections to it. Typically the renormalized value of parameters are close to their fundamental values, but in some cases, it appears that there has been a delicate cancellation between the fundamental quantity and the quantum corrections. Hierarchy problems are related to fine-tuning problems and problems of naturalness.
Studying renormalization in hierarchy problems is difficult, because such quantum corrections are usually power-law divergent, which means that the shortest-distance physics are most important. Because we do not know the precise details of the shortest-distance theory of physics, we cannot even address how this delicate cancellation between two large terms occurs. Therefore, researchers are led to postulate new physical phenomena that resolve hierarchy problems without fine tuning.
The Higgs mass
In particle physics, the most important hierarchy problem is the question that asks why the weak force is 1032 times stronger than gravity. Both of these forces involve constants of nature, Fermi's constant for the weak force and Newton's constant for gravity. Furthermore if the Standard Model is used to calculate the quantum corrections to Fermi's constant, it appears that Fermi's constant is surprisingly large and is expected to be closer to Newton's constant, unless there is a delicate cancellation between the bare value of Fermi's constant and the quantum corrections to it.
More technically, the question is why the Higgs boson is so much lighter than the Planck mass (or the grand unification energy, or a heavy neutrino mass scale): one would expect that the large quantum contributions to the square of the Higgs boson mass would inevitably make the mass huge, comparable to the scale at which new physics appears, unless there is an incredible fine-tuning cancellation between the quadratic radiative corrections and the bare mass.
It should be remarked that the problem cannot even be formulated in the strict context of the Standard Model, for the Higgs mass cannot be calculated. In a sense, the problem amounts to the worry that a future theory of fundamental particles, in which the Higgs boson mass will be calculable, should not have excessive fine-tunings.
One proposed solution, popular amongst many physicists, is that one may solve the hierarchy problem via supersymmetry. Supersymmetry can explain how a tiny Higgs mass can be protected from quantum corrections. Supersymmetry removes the power-law divergences of the radiative corrections to the Higgs mass and solves the hierarchy problem as long as the supersymmetric particles are light enough to satisfy the Barbieri–Giudice criterion.[2] This still leaves open the mu problem, however. Currently the tenets of supersymmetry are being tested at the LHC, although no evidence has been found so far for supersymmetry.
Theoretical solutions
Supersymmetric solution
Each particle that couples to the Higgs field has a Yukawa coupling λf. The coupling with the Higgs field for fermions gives an interaction term 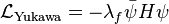 , with
, with 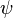 being the Dirac Field and
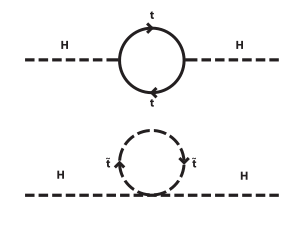
being the Dirac Field and  the Higgs Field. Also, the mass of a fermion is proportional to its Yukawa coupling, meaning that the Higgs boson will couple most to the most massive particle. This means that the most significant corrections to the Higgs mass will originate from the heaviest particles, most prominently the top quark. By applying the Feynman rules, one gets the quantum corrections to the Higgs mass squared from a fermion to be:
the Higgs Field. Also, the mass of a fermion is proportional to its Yukawa coupling, meaning that the Higgs boson will couple most to the most massive particle. This means that the most significant corrections to the Higgs mass will originate from the heaviest particles, most prominently the top quark. By applying the Feynman rules, one gets the quantum corrections to the Higgs mass squared from a fermion to be:
The 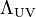 is called the ultraviolet cutoff and is the scale up to which the Standard Model is valid. If we take this scale to be the Planck scale, then we have the quadratically diverging Lagrangian. However, suppose there existed two complex scalars (taken to be spin 0) such that:
is called the ultraviolet cutoff and is the scale up to which the Standard Model is valid. If we take this scale to be the Planck scale, then we have the quadratically diverging Lagrangian. However, suppose there existed two complex scalars (taken to be spin 0) such that:
λS= |λf|2 (the couplings to the Higgs are exactly the same).
Then by the Feynman rules, the correction (from both scalars) is:
(Note that the contribution here is positive. This is because of the spin-statistics theorem, which means that fermions will have a negative contribution and bosons a positive contribution. This fact is exploited.)
This gives a total contribution to the Higgs mass to be zero if we include both the fermionic and bosonic particles. Supersymmetry is an extension of this that creates 'superpartners' for all Standard Model particles.
This section adapted from Stephen P. Martin's "A Supersymmetry Primer" on arXiv.[3]
Conformal solution
Without supersymmetry, a solution to the hierarchy problem has been proposed using just the Standard Model. The idea can be traced back to the fact that the term in the Higgs field that produces the uncontrolled quadratic correction upon renormalization is the quadratic one. If the Higgs field had no mass term, then no hierarchy problem arises. But by missing a quadratic term in the Higgs field, one must find a way to recover the breaking of electroweak symmetry through a non-null vacuum expectation value. This can be obtained using the Weinberg–Coleman mechanism with terms in the Higgs potential arising from quantum corrections. Mass obtained in this way is far too small with respect to what is seen in accelerator facilities and so a conformal Standard Model needs more than one Higgs particle. This proposal has been put forward in 2006 by Krzysztof Meissner and Hermann Nicolai[4] and is currently under scrutiny. But if no further excitation is observed beyond the one seen so far at LHC, this model would have to be abandoned.
Solution via extra dimensions
If we live in a 3+1 dimensional world, then we calculate the Gravitational Force via Gauss' law for gravity:
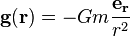 (1)
(1)
which is simply Newton's law of gravitation. Note that Newton's constant G can be rewritten in terms of the Planck mass.
If we extend this idea to 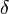 extra dimensions, then we get:
extra dimensions, then we get:
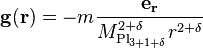 (2)
(2)
where 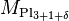 is the 3+1+
is the 3+1+ 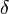 dimensional Planck mass. However, we are assuming that these extra dimensions are the same size as the normal 3+1 dimensions. Let us say that the extra dimensions are of size n <<< than normal dimensions. If we let r << n, then we get (2). However, if we let r >> n, then we get our usual Newton's law. However, when r >> n, the flux in the extra dimensions becomes a constant, because there is no extra room for gravitational flux to flow through. Thus the flux will be proportional to
dimensional Planck mass. However, we are assuming that these extra dimensions are the same size as the normal 3+1 dimensions. Let us say that the extra dimensions are of size n <<< than normal dimensions. If we let r << n, then we get (2). However, if we let r >> n, then we get our usual Newton's law. However, when r >> n, the flux in the extra dimensions becomes a constant, because there is no extra room for gravitational flux to flow through. Thus the flux will be proportional to 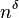 because this is the flux in the extra dimensions. The formula is:
because this is the flux in the extra dimensions. The formula is:
which gives:
Thus the fundamental Planck mass (the extra dimensional one) could actually be small, meaning that gravity is actually strong, but this must be compensated by the number of the extra dimensions and their size. Physically, this means that gravity is weak because there is a loss of flux to the extra dimensions.
This section adapted from "Quantum Field Theory in a Nutshell" by A. Zee.[5]
Braneworld models
In 1998 Nima Arkani-Hamed, Savas Dimopoulos, and Gia Dvali proposed the ADD model, also known as the model with large extra dimensions, an alternative scenario to explain the weakness of gravity relative to the other forces.[6][7] This theory requires that the fields of the Standard Model are confined to a four-dimensional membrane, while gravity propagates in several additional spatial dimensions that are large compared to the Planck scale.[8]
In 1998/99 Merab Gogberashvili published on the arXiv (and subsequently in peer-reviewed journals) a number of articles where he showed that if the Universe is considered as a thin shell (a mathematical synonym for "brane") expanding in 5-dimensional space then it is possible to obtain one scale for particle theory corresponding to the 5-dimensional cosmological constant and Universe thickness, and thus to solve the hierarchy problem.[9][10][11] It was also shown that four-dimensionality of the Universe is the result of stability requirement since the extra component of the Einstein field equations giving the localized solution for matter fields coincides with the one of the conditions of stability.
Subsequently, there were proposed the closely related Randall–Sundrum scenarios which offered their solution to the hierarchy problem.
Finite Groups
It has also been noted that the group order of the Baby Monster group is of the right order of magnitude, 4×1033. It is known that the Monster Group is related to the symmetries of a particular bosonic string theory on the Leech lattice. However, there's no physical reason for why the size of the Monster Group or its subgroups should appear in the Lagrangian. Most physicists think this is merely a coincidence. Another coincidence is that in reduced Plank units, the Higgs mass is approximately 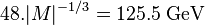 where |M| is the order of the Monster group. This suggests that the smallness of the Higgs mass may be due to a redundancy caused by a symmetry of the extra dimensions, which must be divided out. There are other groups that are also of the right order of magnitude for example
where |M| is the order of the Monster group. This suggests that the smallness of the Higgs mass may be due to a redundancy caused by a symmetry of the extra dimensions, which must be divided out. There are other groups that are also of the right order of magnitude for example 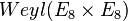 .
.
Empirical tests
Until now, no experimental or observational evidence of extra dimensions has been officially reported. Analyses of results from the Large Hadron Collider severely constrain theories with large extra dimensions.[12]
The cosmological constant
In physical cosmology, current observations in favor of an accelerating universe imply the existence of a tiny, but nonzero cosmological constant. This is a hierarchy problem very similar to that of the Higgs boson mass problem, since the cosmological constant is also very sensitive to quantum corrections. It is complicated, however, by the necessary involvement of general relativity in the problem and may be a clue that we do not understand gravity on long distance scales (such as the size of the universe today). While quintessence has been proposed as an explanation of the acceleration of the Universe, it does not actually address the cosmological constant hierarchy problem in the technical sense of addressing the large quantum corrections. Supersymmetry does not address the cosmological constant problem, since supersymmetry cancels the M4Planck contribution, but not the M2Planck one (quadratically diverging).
See also
References
- ↑ http://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-hierarchy-problem/
- ↑ R. Barbieri, G. F. Giudice (1988). "Upper Bounds on Supersymmetric Particle Masses". Nucl. Phys. B 306: 63. Bibcode:1988NuPhB.306...63B. doi:10.1016/0550-3213(88)90171-X.
- ↑ Stephen P. Martin, A Supersymmetry Primer
- ↑ K. Meissner, H. Nicolai (2006). "Conformal Symmetry and the Standard Model". Physics Letters B648: 312–317. arXiv:hep-th/0612165. Bibcode:2007PhLB..648..312M. doi:10.1016/j.physletb.2007.03.023.
- ↑ Zee, A. (2003). "Quantum field theory in a nutshell". Princeton University Press. Bibcode:2003qftn.book.....Z.
- ↑ N. Arkani-Hamed, S. Dimopoulos, G. Dvali (1998). "The Hierarchy problem and new dimensions at a millimeter". Physics Letters B429: 263–272. arXiv:hep-ph/9803315. Bibcode:1998PhLB..429..263A. doi:10.1016/S0370-2693(98)00466-3.
- ↑ N. Arkani-Hamed, S. Dimopoulos, G. Dvali (1999). "Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity". Physical Review D59: 086004. arXiv:hep-ph/9807344. Bibcode:1999PhRvD..59h6004A. doi:10.1103/PhysRevD.59.086004.
- ↑ For a pedagogical introduction, see M. Shifman (2009). Large Extra Dimensions: Becoming acquainted with an alternative paradigm. Crossing the boundaries: Gauge dynamics at strong coupling. Singapore: World Scientific. arXiv:0907.3074.
- ↑ M. Gogberashvili, Hierarchy problem in the shell universe model, Arxiv:hep-ph/9812296.
- ↑ M. Gogberashvili, Our world as an expanding shell, Arxiv:hep-ph/9812365.
- ↑ M. Gogberashvili, Four dimensionality in noncompact Kaluza-Klein model, Arxiv:hep-ph/9904383.
- ↑ ATLAS Collaboration, "Search for Quantum Black Hole Production in High-Invariant-Mass Lepton+Jet Final States Using pp Collisions at s√=8 TeV and the ATLAS Detector" http://arxiv.org/abs/1311.2006
![\Delta m_{H}^{2} = - \frac{\left|\lambda_{f} \right|^2}{8\pi^2} [\Lambda_{\mathrm{UV}}^2+ ...].](../I/m/286279dd1ebdf509fb10694f9631111f.png)
![\Delta m_{H}^{2} = 2 \times \frac{\lambda_{S}}{16\pi^2} [\Lambda_{\mathrm{UV}}^2+ ...].](../I/m/1f8843d42458934e46ec4a4f0f4dc597.png)