Hidden Markov random field
A hidden Markov random field is a generalization of a hidden Markov model. Instead of having an underlying Markov chain, hidden Markov random fields have an underlying Markov random field.
Suppose that we observe a random variable 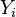 , where
, where 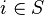 .
Hidden Markov random fields assume that the probabilistic nature of
.
Hidden Markov random fields assume that the probabilistic nature of 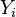 is determined
by the unobservable Markov random field
is determined
by the unobservable Markov random field 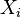 ,
, 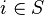 .
That is, given the neighbors
.
That is, given the neighbors 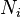 of
of 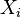 ,
,
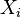 is independent of all other
is independent of all other 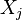 (Markov property).
The main difference with a hidden Markov model is that neighborhood is not defined in 1 dimension
but within a network, i.e.
(Markov property).
The main difference with a hidden Markov model is that neighborhood is not defined in 1 dimension
but within a network, i.e. 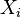 is allowed to have more than the two neighbors
that it would have in a Markov chain.
The model is formulated in such a way that given
is allowed to have more than the two neighbors
that it would have in a Markov chain.
The model is formulated in such a way that given 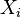 ,
, 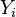 are independent
(conditional independence of the observable variables given the Markov random field).
are independent
(conditional independence of the observable variables given the Markov random field).
See also
- Hidden Markov model
- Markov network
- Bayesian network
References
- Yongyue Zhang; Smith, Stephen; Brady, Michael (11 May 2000). "Hidden Markov Random Field Model". Hidden Markov Random Field Model and Segmentation of Brain MR Images. Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB). FMRIB Technical Report TR00YZ1.