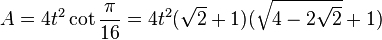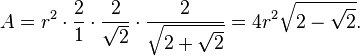Hexadecagon

Regular hexadecagon

A regular hexadecagon
Type Regular polygon
Edges and vertices 16
Schläfli symbol {16}
t{8}
Coxeter diagram
Symmetry group Dihedral (D16), order 2×16
Internal angle (degrees) 157.5°
Dual polygon self
Properties convex, cyclic, equilateral, isogonal, isotoxal

In mathematics, a hexadecagon (sometimes called a hexakaidecagon) is a polygon with 16 sides and 16 vertices.[1]

A regular hexadecagon is a hexadecagon in which all angles are equal and all sides are congruent. Its Schläfli symbol is {16} and can be constructed as a quasiregular truncated octagon, t{8}, which alternates two types of edges.

Construction

As the ancient Greek mathematicians already knew,[2] a regular hexadecagon is constructible using compass and straightedge:


Construction of a regular hexadecagon

Measurements

Each angle of a regular hexadecagon is 157.5 degrees, and the total angle measure of any hexadecagon is 2520 degrees.

The area of a regular hexadecagon is: (with t = edge length)

A = 4t^2 \cot \frac{\pi}{16} = 4t^2 (\sqrt{2}+1)(\sqrt{4-2\sqrt{2}}+1)

Because the hexadecagon has a number of sides that is a power of two, its area can be computed in terms of the circumradius r by truncating Viète's formula:

A=r^2\cdot\frac{2}{1}\cdot\frac{2}{\sqrt{2}}\cdot\frac{2}{\sqrt{2+\sqrt{2}}}=4r^2\sqrt{2-\sqrt{2}}.

Related figures

A hexadecagram is an 16-sided star polygon, represented by symbol {16/n}. There are three regular star polygons, {16/3}, {16/5}, {16/7}, using the same vertices, but connecting every third, fifth or seventh points. There are also three compounds: {16/2} is reduced to 2{8} as two octagons, {16/4} is reduced to 4{4} as four squares and {16/6} reduces to 2{8/3} as two octagrams, and finally {16/8} is reduced to 8{2} as eight digons.

Form Convex polygon Compound Star polygon Compound
Image
{16/1} or {16}
{16/2} or 2{8}
{16/3}
{16/4} or 4{4}
Interior angle 157.5°135°112.5°90°
Form Star polygon Compound Star polygon Compound
Image
{16/5}
{16/6} or 2{8/3}
{16/7}
{16/8} or 8{2}
Interior angle 67.5°45°22.5°0°

Deeper truncations of the regular octagon and octagram can produce isogonal (vertex-transitive) intermediate hexadecagram forms with equally spaced vertices and two edge lengths. [3]

A truncated octagon is a hexadecagon, t{8}={16}. A quasitruncated octagon, inverted as {8/7}, is a hexadecagram: t{8/7}={16/7}. A truncated octagram {8/3} is a hexadecagram: t{8/3}={16/3} and a quasitruncated octagram, inverted as {8/5}, is a hexadecagram: t{8/5}={16/5}.

Isogonal truncations of octagon and octagram: {8}, {8/3}
Quasiregular Isogonal Quasiregular

t{8}={16}
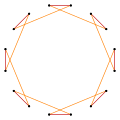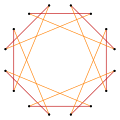t{8/7}={16/7}

t{8/3}={16/3}
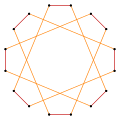t{8/5}={16/5}

Petrie polygons

The regular hexadecagon is the Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections, including:

A15 B8 D9 2B2 (4D)

15-simplex
8-orthoplex
8-cube
611
161
8-8 duopyramid
8-8 duoprism

In art

The hexadecagonal tower from Raphael's The Marriage of the Virgin

In the early 16th century, Raphael was the first to construct a perspective image of a regular hexadecagon: the tower in his painting The Marriage of the Virgin has 16 sides, elaborating on an eight-sided tower in a previous painting by Pietro Perugino.[4]

A hexadecagrammic pattern from the Alhambra

Hexadecagrams, 16-pointed star polygons, are included in the Girih patterns in the Alhambra.[5]

Irregular hexadecagons

An octagonal star can be seen as a concave hexadecagon:

References

  1. ↑ Weisstein, Eric W. (2002). CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. p. 1365. ISBN 9781420035223.
  2. ↑ Koshy, Thomas (2007), Elementary Number Theory with Applications (2nd ed.), Academic Press, p. 142, ISBN 9780080547091.
  3. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
  4. ↑ Speiser, David (2011), "Architecture, mathematics and theology in Raphael’s paintings", Crossroads: History of Science, History of Art. Essays by David Speiser, vol. II, Springer, pp. 29–39, doi:10.1007/978-3-0348-0139-3_3 |first1= missing |last1= in Editors list (help) . Originally published in Nexus III: Architecture and Mathematics, Kim Williams, ed. (Ospedaletto, Pisa: Pacini Editore, 2000), pp. 147–156.
  5. ↑ Hankin, E. Hanbury (May 1925), "Examples of methods of drawing geometrical arabesque patterns", The Mathematical Gazette 12 (176): 370–373, doi:10.2307/3604213.

External links