Hermitian matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a square matrix with complex entries that is equal to its own conjugate transpose—that is, the element in the i-th row and j-th column is equal to the complex conjugate of the element in the j-th row and i-th column, for all indices i and j:
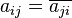 or
or  , in matrix form.
, in matrix form.
Hermitian matrices can be understood as the complex extension of real symmetric matrices.
If the conjugate transpose of a matrix  is denoted by
is denoted by 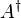 , then the Hermitian property can be written concisely as
, then the Hermitian property can be written concisely as
Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues.
Examples
See the following example:
The diagonal elements must be real, as they must be their own complex conjugate.
Well-known families of Pauli matrices, Gell-Mann matrices and their generalizations are Hermitian. In theoretical physics such Hermitian matrices are often multiplied by imaginary coefficients,[1][2] which results in skew-Hermitian matrices (see below).
Here we offer another useful Hermitian matrix using an abstract example.
If a square matrix  equals the multiplication of a matrix and its conjugate transpose, that is,
equals the multiplication of a matrix and its conjugate transpose, that is, 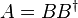 , then
, then  is a Hermitian positive semi-definite matrix. Furthermore, if
is a Hermitian positive semi-definite matrix. Furthermore, if 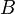 is row full-rank, then
is row full-rank, then  is positive definite.
is positive definite.
Properties
- The entries on the main diagonal (top left to bottom right) of any Hermitian matrix are necessarily real, because they have to be equal to their complex conjugate.
- Because of conjugation, for complex valued entries the off diagonal entries cannot be symmetric (or same). Hence, a matrix that has only real entries is Hermitian if and only if it is a symmetric matrix, i.e., if it is symmetric with respect to the main diagonal. A real and symmetric matrix is simply a special case of a Hermitian matrix.
- Every Hermitian matrix is a normal matrix.
- The finite-dimensional spectral theorem says that any Hermitian matrix can be diagonalized by a unitary matrix, and that the resulting diagonal matrix has only real entries. This implies that all eigenvalues of a Hermitian matrix A are real, and that A has n linearly independent eigenvectors. Moreover, it is possible to find an orthonormal basis of Cn consisting of n eigenvectors of A.
- The sum of any two Hermitian matrices is Hermitian, and the inverse of an invertible Hermitian matrix is Hermitian as well. However, the product of two Hermitian matrices A and B is Hermitian if and only if AB = BA. Thus An is Hermitian if A is Hermitian and n is an integer.
- For an arbitrary complex valued vector v the product
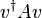 is real because of
is real because of 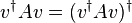 . This is especially important in quantum physics where hermitian matrices are operators that measure properties of a system e.g. total spin which have to be real.
. This is especially important in quantum physics where hermitian matrices are operators that measure properties of a system e.g. total spin which have to be real.
- The Hermitian complex n-by-n matrices do not form a vector space over the complex numbers, since the identity matrix In is Hermitian, but i In is not. However the complex Hermitian matrices do form a vector space over the real numbers R. In the 2n2-dimensional vector space of complex n × n matrices over R, the complex Hermitian matrices form a subspace of dimension n2. If Ejk denotes the n-by-n matrix with a 1 in the j,k position and zeros elsewhere, a basis can be described as follows:
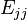 for
for 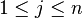 (n matrices)
(n matrices)
- together with the set of matrices of the form
 for
for 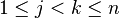 (n2 − n/2 matrices)
(n2 − n/2 matrices)
- and the matrices
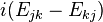 for
for 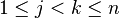 (n2 − n/2 matrices)
(n2 − n/2 matrices)
- where
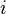 denotes the complex number
denotes the complex number 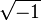 , known as the imaginary unit.
, known as the imaginary unit.
- If n orthonormal eigenvectors
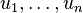 of a Hermitian matrix are chosen and written as the columns of the matrix U, then one eigendecomposition of A is
of a Hermitian matrix are chosen and written as the columns of the matrix U, then one eigendecomposition of A is 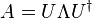 where
where  and therefore
and therefore
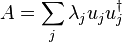 ,
,
- where
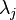 are the eigenvalues on the diagonal of the diagonal matrix
are the eigenvalues on the diagonal of the diagonal matrix 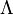 .
.
Further properties
Additional facts related to Hermitian matrices include:
- The sum of a square matrix and its conjugate transpose
 is Hermitian.
is Hermitian. - The difference of a square matrix and its conjugate transpose
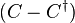 is skew-Hermitian (also called antihermitian). This implies that commutator of two Hermitian matrices is skew-Hermitian.
is skew-Hermitian (also called antihermitian). This implies that commutator of two Hermitian matrices is skew-Hermitian. - An arbitrary square matrix C can be written as the sum of a Hermitian matrix A and a skew-Hermitian matrix B:
- The determinant of a Hermitian matrix is real:
- Proof:
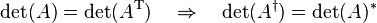
- Therefore if

- Proof:
- (Alternatively, the determinant is the product of the matrix's eigenvalues, and as mentioned before, the eigenvalues of a Hermitian matrix are real.)
Rayleigh quotient
See also
- Skew-Hermitian matrix (anti-Hermitian matrix)
- Haynsworth inertia additivity formula
- Hermitian form
- Self-adjoint operator
- Unitary matrix
References
- ↑ Frankel, Theodore (2004). The geometry of physics: an introduction. Cambridge University Press. p. 652. ISBN 0-521-53927-7.
- ↑ Physics 125 Course Notes at California Institute of Technology
External links
- Hazewinkel, Michiel, ed. (2001), "Hermitian matrix", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Visualizing Hermitian Matrix as An Ellipse with Dr. Geo, by Chao-Kuei Hung from Shu-Te University, gives a more geometric explanation.
- "Hermitian Matrices" at MathPages.com.


