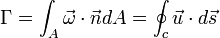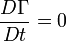Helmholtz's theorems
In fluid mechanics, Helmholtz's theorems, named after Hermann von Helmholtz, describe the three-dimensional motion of fluid in the vicinity of vortex filaments. These theorems apply to inviscid flows and flows where the influence of viscous forces are small and can be ignored.
Helmholtz’s three theorems are as follows:[1]
Helmholtz’s first theorem:
- The strength of a vortex filament is constant along its length.
Helmholtz’s second theorem:
- A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path.
Helmholtz’s third theorem:
- In the absence of rotational external forces, a fluid that is initially irrotational remains irrotational.
Helmholtz’s theorems apply to inviscid flows. In observations of vortices in real fluids the strength of the vortices always decays gradually due to the dissipative effect of viscous forces.
Alternative expressions of the three theorems are as follows:
1. The strength of a vortex tube does not vary with time.[2]
2. Fluid elements lying on a vortex line at some instant continue to lie on that vortex line. More simply, vortex lines move with the fluid. Also vortex lines and tubes must appear as a closed loop, extend to infinity or start/end at solid boundaries.
3. Fluid elements initially free of vorticity remain free of vorticity.
Helmholtz’s theorems have application in understanding:
Helmholtz’s theorems are now generally proven with reference to Kelvin's circulation theorem. However the Helmholtz's theorems were published in 1858, nine years before the 1867 publication of Kelvin's theorem. There was much communication between the two men on the subject of vortex lines, with many references to the application of their theorems to the study of smoke rings.
Notes
- ↑ Kuethe and Schetzer, Foundations of Aerodynamics, Section 2.14
- ↑ The strength of a vortex tube (circulation), is defined as:
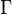 is also the circulation,
is also the circulation, 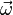 is the vorticity vector,
is the vorticity vector, 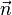 is the normal vector to a surface A, formed by taking a cross-section of the vortex-tube with elemental area dA,
is the normal vector to a surface A, formed by taking a cross-section of the vortex-tube with elemental area dA, 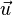 is the velocity vector on the closed curve C, which bounds the surface A. The convention for defining the sense of circulation and the normal to the surface A is given by the right-hand screw rule. The third theorem states that this strength is the same for all cross-sections A of the tube and is independent of time. This is equivalent to saying
is the velocity vector on the closed curve C, which bounds the surface A. The convention for defining the sense of circulation and the normal to the surface A is given by the right-hand screw rule. The third theorem states that this strength is the same for all cross-sections A of the tube and is independent of time. This is equivalent to saying
-
References
- M. J. Lighthill, An Informal Introduction to Theoretical Fluid Mechanics, Oxford University Press, 1986, ISBN 0-19-853630-5
- P. G. Saffman, Vortex Dynamics, Cambridge University Press, 1995, ISBN 0-521-42058-X
- G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge University Press (1967, reprinted in 2000).
- Kundu, P and Cohen, I, Fluid Mechanics, 2nd edition, Academic Press 2002.
- George B. Arfken and Hans J. Weber, Mathematical Methods for Physicists, 4th edition, Academic Press: San Diego (1995) pp. 92–93
- A.M. Kuethe and J.D. Schetzer (1959), Foundations of Aerodynamics, 2nd edition. John Wiley & Sons, Inc. New York ISBN 0-471-50952-3