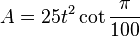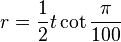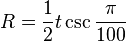Hectogon

Regular hectogon

A regular hectogon
Type Regular polygon
Edges and vertices 100
Schläfli symbol {100}
t{50}
Coxeter diagram
Symmetry group Dihedral (D100), order 2×100
Internal angle (degrees) 176.4°
Dual polygon self
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a hectogon or hecatontagon[1][2] is a hundred-sided polygon.[3][4] The sum of any hectogon's interior angles is 17640 degrees.

A regular hectogon is represented by Schläfli symbol {100} and can be constructed as a quasiregular truncated pentacontagon, t{50}, which alternates two types of edges.

Regular hectogon properties

One interior angle in a regular hectogon is 176.4°, meaning that one exterior angle would be 3.6°.

The area of a regular hectogon is (with t = edge length)

A = 25t^2 \cot \frac{\pi}{100}

and its inradius is

r = \frac{1}{2}t \cot \frac{\pi}{100}

The circumradius of a regular hectogon is

R = \frac{1}{2}t \csc \frac{\pi}{100}

A regular hectogon is not constructible using a compass and straightedge,[5] and is not constructible even if the use of an angle trisector is allowed.[6]

Hectogram

A hectogram is an 100-sided star polygon. There are 19 regular forms[7] given by Schläfli symbols {100/3}, {100/7}, {100/9}, {100/11}, {100/13}, {100/17}, {100/19}, {100/21}, {100/23}, {100/27}, {100/29}, {100/31}, {100/33}, {100/37}, {100/39}, {100/41}, {100/43}, {100/47}, and {100/49}, as well as 30 regular star figures with the same vertex configuration.

Regular star polygons {100/k}
Picture
{100/3}
{100/7}
{100/11}
{100/13}
{100/17}
{100/19}
Interior angle 169.2° 154.8° 140.4° 133.2° 118.8° 111.6°
Picture
{100/21}
{100/23}
{100/27}
{100/29}
{100/31}
{100/37}		  
104.4° 97.2° 82.8° 75.6° 68.4° 46.8°  
Picture
{100/39}
{100/41}
{100/43}
{100/47}
{100/49}		  
Interior angle 39.6° 32.4° 25.2° 10.8° 3.6°  

References

  1. ↑
  2. ↑
  3. ↑ Gorini, Catherine A. (2009), The Facts on File Geometry Handbook, Infobase Publishing, p. 110, ISBN 9781438109572.
  4. ↑ The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
  5. ↑ Constructible Polygon
  6. ↑ http://www.math.iastate.edu/thesisarchive/MSM/EekhoffMSMSS07.pdf
  7. ↑ 19 = 50 cases - 1 (convex) - 10 (multiples of 5) - 25 (multiples of 2)+ 5 (multiples of 2 and 5)