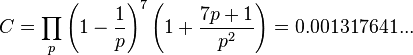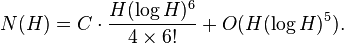Heath-Brown–Moroz constant

The Heath-Brown–Moroz constant C,[1] named for Roger Heath-Brown and Boris Moroz, is defined as

C=\prod_p\left(1-\frac{1}{p}\right)^7\left(1+\frac{7p+1}{p^2}\right) = 0.001317641...

where p runs over the primes.

This constant is part of an asymptotic estimate for the distribution of rational points of bounded height on the cubic surface X03=X1X2X3. Let H be a positive real number and N(H) the number of solutions to the equation X03=X1X2X3 with all the Xi non-negative integers less than or equal to H and their greatest common divisor equal to 1. Then

N(H)= C \cdot \frac{H(\log H)^6} {4\times 6!} + O(H(\log H)^5).

References

  1. ↑ D. R. Heath-Brown; B.Z. Moroz (1999). "The density of rational points on the cubic surface X03=X1X2X3". Mathematical Proceedings of the Cambridge Philosophical Society 125 (3): 385–395. doi:10.1017/S0305004198003089.